Atomo ir branduolio fizika "Fizikos Olimpo" moksleiviams
|
|
|
- Ričardas Stankevičius
- prieš 6 metus
- Peržiūrų:
Transkriptas
1 Interneto nuoroda į tinklalapį su paskaitų konspektais ir uždavinių sąlygomis: Interneto nuorodą į tinklalapį, kuriame yra pdf failai su laboratorinių darbų aprašais: Atomas Atomo ir branduolio sandara ir pagrindinės savybės Branduolys Sudarytas iš elektronų ir branduolio. Elektrono masė m e = 9, kg, branduolio masė ~( ) kg, Elektrono krūvis e = C, branduolio krūvis +Ze Elektrono sukinio kvantinis skaičius s = 1/ Elektrono magnetinis momentas J T 1 Sudarytas ir protonų ir neutronų (nukleonų). Protono masė m p = kg = a.m.v., neutrono masė m n = kg = a.m.v. Protono elektros krūvis +e, neutrono elektros krūvis. Nukleono sukinio kvantinis skaičius s = 1/ Protono magnetinis momentas J T 1 Neutrono magnetinis momentas J T 1 Matmenys ~1 Å (1 1 m). Matmenys ( ) m. Tipiški intervalai tarp energijos lygmenų ~(1 1) ev. Egzistuoja tik elektromagnetinė sąveika. Branduolys pasireiškia tik kaip taškinis krūvis. Elektromagnetinė sąveika yra toliasiekė. Galimi savaiminiai virsmai: Kvantinis šuolis į žemesnį energijos lygmenį, išspinduliuojant fotoną arba elektroną Galimi pokyčiai dėl susidūrimo su dalele: kvantinis šuolis į kitą energijos lygmenį, vieno arba kelių elektronų netekimas, elektrono pagavimas. Galimi žymūs elektronų konfigūracijos pokyčiai dėl sąveikos su aplinkiniais atomais (pvz., cheminių ryšių susidarymas) Tipiški intervalai tarp energijos lygmenų ~(1 1) MeV. Tarp nukleonų veikia branduolinės traukos jėga, o protonai sąveikauja dar ir elektrinėmis jėgomis. Branduolinė sąveika yra artisiekė (~1 15 m). Galimi savaiminiai virsmai: Kvantinis šuolis į žemesnį energijos lygmenį, išspinduliuojant fotoną arba išlaisvinant atomo elektroną, neutrono virsmas protonu arba atvirkščiai, atomo elektrono pagavimas, alfa dalelių ( 4 He branduolių) emisija, savaiminis dalijimasis, kai didelė sužadinimo energija neutronų, protonų ir kitų branduolių emisija Galimi pokyčiai dėl susidūrimo su dalele: Sužadinimas į aukštesnį energijos lygmenį, nukleonų arba branduolių emisija, dalelės pagavimas, dalijimasis, fotonų emisija, elektronų išlaisvinimas iš atomo Palyginti maža aplinkinių atomų įtaka Terminai ir žymėjimai: branduolio krūvio skaičius Z protonų skaičius branduolyje (sutampa su atominiu numeriu), branduolio masės skaičius A protonų ir neutronų skaičių suma: A = Z + N, nuklidas cheminio elemento atomų rūšis su apibrėžtais masės ir krūvio skaičiais ir su apibrėžta energija, izotopai nuklidai su vienodais Z, bet su skirtingais A, izobarai nuklidai su vienodais A, bet su skirtingais Z, izotonai nuklidai su vienodu neutronų skaičiumi branduolyje, bet su skirtingais Z. Nuklido žymėjimas: A Z X, čia X yra cheminio elemento simbolis (pvz., 38 U yra vienas iš urano izotopų). 9 1
2 Kvantinės mechanikos pradmenys Banginė funkcija. De Broilio bangos. Neapibrėžtumų sąryšis Dalelės banginė funkcija tai koordinačių ir laiko kompleksinė funkcija (x,y,z,t), kuri apibūdina dalelės judėjimo būseną ir kurios modulio kvadratas lygus tikimybės tankiui aptikti duotosios būsenos dalelę erdvės taške su koordinatėmis x, y ir z laiko momentu t: dp dv arba d P dv. Tikimybės tankis: dp/dv. P d P dv Banginės funkcijos normavimo sąlyga:. V V dv 1. Superpozicijos principas: dalelės banginė funkcija yra lygi funkcijų, atitinkančių visus galimus įvykius, tiesiniam dariniui: N a. Dėl superpozicijos principo vyksta materialiųjų dalelių interferencija ir difrakcija. Dalelės banginių ir dalelinių savybių sąryšis: E h h, h p, p hk. Taigi, bet kuri laisvoji dalelė, kuri turi impulsą, yra susijusi su banga, kurios ilgis yra h h p m, v o bangos skaičius lygus p me k. h h Šios bangos vadinamos de Broilio bangomis. Neapibrėžtumų sąryšis (Heizenbergo nelygybė): xp x h čia x yra dalelės koordinatės neapibrėžtumas (standartinis nuokrypis), p x yra atitinkamos impulso 34 komponentės neapibrėžtumas, o h h /(π) 1,5 1 J s yra mažoji Planko konstanta. x v x h. m Neapibrėžtumų sąryšis reiškia, kad dalelės judėjimo trajektorijos sąvoka, kuri vartojama klasikinėje mechanikoje, netinka mikrodalelių judėjimui apibūdinti. Heizenbergo nelygybė tapo vienu iš pagrindinių kvantinės mechanikos principų. Kvantinė mechanika tai fizikos šaka, kuri tiria mikrodalelių judėjimo išorinių jėgų laukuose dėsnius ir tų dalelių sistemų (pvz., atomų, molekulių, kristalų) vidines savybes. i i i
3 Surištų mikrodalelių energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje 8 8 U = 8 U = U = 8 x = x= w Begalinio gylio stačiakampė potencialo duobė. Dalelė gali laisvai judėti erdvės srityje x w, tačiau negali būti erdvės srityse x < ir x > w. Apačioje pavaizduotas tokios sistemos klasikinis analogas: rutuliukas, kuris slysta be trinties išilgai vielos ir tampriai atšoka nuo kietų sienų taškuose x = ir x = w, xw; U( x), x ir x w. Pagal banginės funkcijos statistinę sampratą (x), kai x < arba x > w. Banginės funkcijos kraštinės sąlygos: () =, (w) =. Stovinčiosios bangos bendroji išraiška yra ( x) Asinkx Bcoskx. 1) A sin() B cos() = B =, ) A sin kw B cos kw = A sin kw cos kw = A sin kw =. Iš pirmosios sąlygos ( x) Asinkx. Iš antrosios sąlygos A = arba sin kw =. Tačiau A negali būti lygus nuliui, todėl sin kw =, t. y. kw nπ (n =, ±1, ±, ). Vertę n = reikia atmesti, nes tada k = ir (x). p h k π h E n (n = 1,, 3,...). m m mw Daugiklis A apskaičiuojamas remiantis normavimo sąlyga w ( x)dx 1. A. w nπ ( x) n ( x) sin x ( n 1,,3...). w w 3
4 Kraštinės sąlygos kubinės begalinio gylio potencialo duobės atveju: (, yz, ), ( wyz,, ) ; ( x,, z), ( x, w, z) ; ( xy,,), ( xyw,, ). E = E x E y E z, h E En nx ny nz (n x, n y, n z = 1,, 3, ), 8mw 3 nx, ny, nz x y z ( x, yz, ) ( x) sinkxsinkysinkz; w čia nx π ny kx, π nz ky, k π z. w w w Sveikieji skaičiai n x, n y, n z tai kvantinių skaičių pavyzdys. Taip vadinami skaičiai, kurie nusako sistemos kvantinę būseną (t. y. banginę funkciją). Jų kiekis, prasmė ir galimos vertės priklauso nuo konkrečios sistemos. 4
5 Realistiškų potencialo duobių pavyzdžiai Neutrono (a) ir protono (b) potencinės energijos priklausomybė nuo atstumo iki branduolio centro. Už branduolio ribų protoną veikia tik Kulono stūmos jėga, kurią atitinka potencinė energija U = Ze / (4π r). Ištisinis spektras (E > ) r Energija E U(r) E 1 Vandenilio atomo potencinė energija ir energijos lygmenys Vandenilio atomo arba jono, kuris turi tik vieną elektroną (apibendrintai vandeniliškojo atomo ), elektrono banginė funkcija, kai elektronas yra žemiausiame energijos lygmenyje: 1 r 1() r exp. 3 πr r1 1 5
6 Centriniame jėgų lauke esančio elektrono arba nukleono kvantiniai skaičiai Centriniame jėgų lauke esančios dalelės erdvinio judėjimo būseną nusako trys dydžiai: 1) dalelės energija, ) dalelės judesio kiekio momento (taip pat vadinamo impulso momentu) modulis, 3) dalelės judesio kiekio momento projekcija į laisvai pasirinktą kryptį. Kiekvieną iš šių dydžių atitinka tam tikras kvantinis skaičius. Orbitinio judesio kiekio momento modulį L nusako orbitinis kvantinis skaičius l (kitas pavadinimas šalutinis kvantinis skaičius): L h ll ( 1) ( l,1,,...) Orbitinio impulso momento vektoriaus L projekciją nusako magnetinis kvantinis skaičius m l : Lz mlh ( ml l, l1,... l1, l) Kai nėra išorinių (branduolio atžvilgiu) laukų ir nepaisoma nukleono sukinio, tada nukleono energija nepriklauso nuo m l. z l = z L z L L z L Galimi kampai tarp judesio kiekio Judesio kiekio momento vektoriaus momento ir išskirtosios krypties precesija aplink išskirtąją kryptį Kiekvieną l ir m l porą atitinka kelios galimos energijos. Tos energijos numeruojamos energijos didėjimo kryptimi. Šitaip apibrėžtas numeris žymimas n. Tai yra pagrindinis kvantinis skaičius. Vietoj l verčių (, 1,,...) vartojamos raidės atitinkamai s, p, d, f, g,... Pvz., jeigu nukleono n =, o l = 1, tada sakoma p nukleonas. Pilnai apibūdinant nukleono būseną, reikia įskaityti jo sukinį vidinį impulso momentą. Nukleono sukinio kvantinis skaičius: 1 s Sukininio judesio kiekio momento modulis: 3 L s h ss ( 1) h Sukinio magnetinis kvantinis skaičius m s nusako sukininio judesio kiekio momento projekciją: L m h ( m s 1/ ) sz s s 6
7 Jeigu neatsižvelgiama į sąveikas, kurias lemia nukleono sukinys, tada nukleono būseną galima pilnai nusakyti šiais keturiais kvantiniais skaičiais: n, l, m l, m s. Skaičiai m l ir m s netinka, jeigu yra atsižvelgiama į sąveikas, kurias lemia sukinys (pvz., sukinio ir orbitos sąveika). Tada vietoj m l ir m s reikia naudoti pilnutinio judesio kiekio momento kvantinį skaičių j ir pilnutinio judesio kiekio projekcijos kvantinį skaičių m j. Nukleono pilnutinio judesio kiekio momento vektorius: Lj L L s Bendroji kvantinės mechanikos impulso momentų sudėties taisyklė: jeigu sudedamųjų momentų modulius nusako kvantiniai skaičiai l 1 ir l, o projekcijas nusako kvantiniai skaičiai m 1 ir m, tada suminio momento modulio galimos vertės yra L h l( l 1) ( l l1l, l1l 1,..., l1l), o jo projekcija lygi Lz L1z Lz mh ( m m1m) Taikant šią taisyklę nukleono orbitinio (l 1 l, m 1 m l ) ir sukininio (l s = 1/, m m s ) judesio kiekio momentų sudėčiai, gaunama, kad pilnutinio momento L j modulio galimosios vertės yra: L j h j( j1) kur kvantinis skaičius j gali būti lygus tik šioms vertėms: 1 a) jeigu l >, j l ; 1 b) jeigu l =, j Pilnutinio judesio kiekio momento projekcija: Ljz mjh ( mj j, j1,..., j1, j) j vertė nurodoma apatinio indekso pavidalu, pvz., p 3/. z Lj L L j L L jz L j L s L s L s L Du galimi kampai tarp nukleono sukinio vektoriaus L s ir nukleono orbitinio judesio kiekio momento vektoriaus L bei atitinkami nukleono pilnutinio judesio kiekio momento vektoriai L j Nukleono sukininio judesio kiekio momento vektoriaus L s ir orbitinio judesio kiekio momento vektoriaus L precesija aplink pilnutinio judesio kiekio momento vektorių L j ir pastarojo vektoriaus precesija aplink išskirtąją kryptį Z 7
8 Banginės funkcijos pavidalas Naudojant sferines koordinates, banginę funkciją galima išreikšti trijų funkcijų, kurių kiekviena priklauso nuo vienos sferinės koordinatės, sandauga: (, r, ) X() r P() () X() r Y(, ) X(r) radialioji banginė funkcija, Y(, ) kampinė banginė funkcija. Jų prasmės aiškinimas išplaukia iš banginė funkcijos statistinio aiškinimo. Tam visų pirma apibrėžiame tūrio elementą: dv r sin drdd Tikimybė, kad nukleonas priklausys tam tūrio elementui: ( r,, ) d V X( r) r d r Y(, ) sindd Vadinasi, X( r) r yra radialinis tikimybės tankis, o Y (, ) yra kampinis tikimybės tankis. Dekarto ir sferinių koordinačių sąryšis Nuo U(r) priklauso tik X(r). Y(, ) yra sferinės harmonikos. Kiekvieną l ir m l porą atitinka tam tikra sferinė harmonika Y (, ). Sferinė harmonika, kuri atitinka l =, yra konstanta: lm l 1 Y π Kai l >, Y(, ) nėra konstanta, t. y. nukleono pasiskirstymas aplink branduolio centrą nėra sferiškai simetriškas: z l = 1 m l = m l = ± 1 x p nukleonų erdvinio tikimybės tankio kampinė dalis Y(,), atitinkanti tris kvantinio skaičiaus m l vertes. Y(,) vertę įvairiomis kryptimis nusako atstumai nuo koordinačių centro iki pavaizduotų paviršių 8
9 Tapatingų dalelių sistemos Kvantinėje mechanikoje vienodų (tapatingų) dalelių neįmanoma sunumeruoti ir sekti kiekvienos jų judėjimą laike (kaip klasikinėje mechanikoje). Tiksliau, jeigu kvantinę sistemą sudaro tapatingos dalelės, tada galima kalbėti tik apie tam tikros būsenos dalelių skaičių, tačiau neįmanoma konkrečiai pasakyti, kuri iš tų dalelių yra kurios būsenos. Be to, kvantinėje mechanikoje įrodoma, kad tapatingų dalelių sistemų savybės priklauso nuo to, ar dalelių sukinio kvantinis skaičius (trumpiau sukinys) yra sveikasis skaičius (bozonai), ar pusinis skaičius (fermionai). Fermionams galioja Paulio draudimo principas: sistemoje negali būti du vienodi fermionai, kurių visi atitinkami kvantiniai skaičiai sutampa. Energijos minimumo principas teigia, kad, esant duotam fermionų skaičiui sistemoje, jų pasiskirstymas tarp viendalelių kvantinių būsenų yra toks, kad sistemos energija būtų mažiausia. Dažnai vietoj kvantinių būsenų patogiau kalbėti apie energijos lygmenis. Skirtingų kvantinių būsenų energijos kartais būna vienodos, t. y. viename energijos lygmenyje gali būti keli skirtingų kvantinių būsenų fermionai. Pvz., sferinės siomtrijos atveju dalelės energija nepriklauso nuo kvantinio skaičiaus m j, kuris gali įgyti j + 1 verčių: mj j, j1,..., j 1, j. Tada viename energijos lygmenyje gali būti iki j + 1 vienodų fermionų (pvz., elektronų arba nukleonų). Atomo elektronų arba branduolio nukleonų pasiskirstymas tarp viendalelių būsenų vadinamas atomo arba branduolio konfigūracija. Užrašant konfigūraciją, dalelių skaičius lygmenyje nurodomas viršutinio indekso pavidalu. Deguonies izotopo 17 O pagrindinės būsenos neutronų posistemės konfigūracija: (1s 1/ ) (1p 3/ ) 4 (1p 1/ ) (1d 5/ ) 1 Elektronų sluoksniai atome Atomo fizikoje elektrono erdvinio judėjimo būsena, kuri atitinka apibrėžtą kvantinių skaičių trejetą n, l, m l, vadinama orbitale. Apytikslėje analizėje (kai nepaisoma sukinio ir orbitos sąveikos) kiekvieną energijos lygmenį galima nusakyti tik dviem kvantiniais skaičiais n ir l. Pagal vandenilio atomo modelį, kurį suformulavo Boras, elektronas, kurio pagrindinis kvantinis skaičius yra n, juda aplink branduolį apskrita orbita, kurios spindulys yra h,59 Å rn n n. πmze Z Atitinkama elektrono energija yra 9
10 4 Z me 1 h Z En 13,6 ev ( n1,, 3,...). n 8 h n r1 m n Jeigu atome yra daugiau negu vienas elektronas, tada dėl elektronų tarpusavio sąveikos elektrono energija priklauso ir nuo l (tačiau silpniau, negu nuo n). Priklausomybės nuo l priežastis ekranavimo reiškinys, kai arčiau branduolio esantys elektronai ekranuoja branduolio krūvį ir taip sumažina efektinį krūvį, kuris veikia toliau esančius elektronus. Elektrono radialusis tikimybės tankis X ( r) r Energija (ev) l = l = 1 l = l = 3 l = 4 5s 5p 5d 5f 5g 1 4s 4p 4d 4f 3p 3d s s p Ličio lygmenys Pagrindinė būsena n = 5 n = 4 n = 3 Vandenilio lygmenys n = 1s, s ir p elektronų radialieji tikimybės tankiai (r 1 yra pirmasis Boro spindulys). Viršuje parodyta s ir p elektronų erdvinių pasiskirstymų dalis, kuri yra viduje sferos su spinduliu r 1 Ličio (Li) atomo valentinio elektrono energijos lygmenų diagrama Ekranavimo reiškinys yra svarbus, aiškinant periodinę elementų sistemą. Orbitalės, kurių pagrindinis kvantinis skaičius n sutampa, sudaro elektronų sluoksnį. orbitalės, kurių n ir l sutampa, sudaro elektronų posluoksnį (pogrupį). Elektronų sluoksniai žymimi raidėmis K, L, M ir t. t. Elektronų posluoksniai žymimi raidėmis s, p, d, f, g, Elektronų sluoksnių žymenys Pagrindinis kvantinis skaičius n Elektronų sluoksnis K L M N O Elektronų posluoksnių žymenys Šalutinis kvantinis skaičius l Elektronų posluoksnis s p d f g 1
11 Viename posluoksnyje gali būti ne daugiau kaip (l1) elektronų. Didžiausias galimas elektronų skaičius n-tajame sluoksnyje yra n1 (l1) n. l Didžiausi elektronų skaičiai sluoksniuose ir posluoksniuose Sluoksnis n Didžiausias elektronų skaičius posluoksnyje Iš viso sluoksnyje s p d f g K 1 L 6 8 M N O Idealioji sluoksnių užpildymo tvarka: kiekvienas prisijungęs elektronas užima orbitalę su mažiausiais n ir l, kuriuos leidžia Paulio draudimo principas. Kai elektronų sluoksnis yra pilnai užpildytas, susidaro stabili elektronų konfigūracija, kuri atitinka inertinių dujų elektronų konfigūraciją. Paskui prasideda kito sluoksnio užpildymas (pradedant nuo šarminio metalo). Pilnai užpildyto posluoksnio pilnutiniai orbitinis ir sukininis impulso momentai lygūs nuliui. Todėl atomo fizikines ir chemines savybes lemia išorinių (iš dalies užpildytų) sluoksnių elektronai. Jeigu ir išorinis sluoksnis yra pilnai užpildytas, tada cheminis elementas yra inertinės dujos. Nukrypimai nuo idealiosios užpildymo tvarkos pasireiškia dėl minėtojo ekranavimo efekto: Po argono ( 18 Ar), kurio konfigūracija yra (Ne) 3s 3p 6, pagal idealiąją tvarką turėtų būti elementas, kurio konfigūracija (Ar) 3d. Tačiau kalio 19 K konfigūracija yra (Ar) 4s, nes kalio 4s būsenos elektrono energija yra mažesnė už 3d būsenos elektrono energiją. 11
12 Periodinė elementų sistema ir atomų elektronų konfigūracijos Z Elementas A Pagrindinės būsenos konfigūracija Pagr. būs. Joniz. en.(ev) 1 H Vandenilis 1,794 1s S 1/ 13,5984 He Helis 4,6 1s 1 S 4, Li Litis 6,941 1s s S 1/ 5, Be Berilis 9,118 1s s 1 S 9,37 5 B Boras 1,811 1s s p P 1/ 8,98 6 C Anglis 1,17 1s s p 3 P 11,63 7 N Azotas 14,674 1s s p 3 4 S 3/ 14, O Deguonis 15,9994 1s s p 4 3 P 13, F Fluoras 18,9984 1s s p 5 P 3/ 17,48 1 Ne Neonas,1797 1s s p 6 1 S 1, Na Natris,98977 (Ne) 3s S 1/ 5, Mg Magnis 4,35 (Ne) 3s 1 S 7, Al Aliuminis 6,98154 (Ne) 3s 3p P 1/ 5, Si Silicis 8,855 (Ne) 3s 3p 3 P 8, P Fosforas 3,97376 (Ne) 3s 3p 3 4 S 3/ 1, S Siera 3,66 (Ne) 3s 3p 4 3 P 1,36 17 Cl Chloras 35,453 (Ne) 3s 3p 5 P 3/ 1, Ar Argonas 39,948 (Ne) 3s 3p 6 1 S 15, K Kalis 39,983 (Ar) 4s S 1/ 4,347 Ca Kalcis 4,78 (Ar) 4s 1 S 6,113 1 Sc Skandis 44,95591 (Ar) 3d 4s D 3/ 6,5615 Ti Titanas 47,867 (Ar) 3d 4s 3 F 6,881 3 V Vanadis 5,9415 (Ar) 3d 3 4s 4 F 3/ 6,746 4 Cr Chromas 51,9961 (Ar) 3d 5 4s 7 S 3 6, Mn Manganas 54,9385 (Ar) 3d 5 4s 6 S 5/ 7,434 6 Fe Geležis 55,8457 (Ar) 3d 6 4s 5 D 4 7,94 7 Co Kobaltas 58,933 (Ar) 3d 7 4s 4 F 9/ 7,881 8 Ni Nikelis 58,6934 (Ar) 3d 8 4s 3 F 4 7, Cu Varis 63,546 (Ar) 3d 1 4s S 1/ 7,764 3 Zn Cinkas 65,49 (Ar) 3d 1 4s 1 S 9,394 P e r e i n a m i e j i e l e m en t a i 31 Ga Galis 69,73 (Ar) 3d 1 4s 4p P 1/ 5, Ge Germanis 7,64 (Ar) 3d 1 4s 4p 3 P 7, As Arsenas 74,916 (Ar) 3d 1 4s 4p 3 4 S 3/ 9, Se Selenas 78,96 (Ar) 3d 1 4s 4p 4 3 P 9, Br Bromas 79,94 (Ar) 3d 1 4s 4p 5 P 3/ 11, Kr Kriptonas 83,798 (Ar) 3d 1 4s 4p 6 1 S 13,9996 1
13 Z Elementas A Pagrindinės būsenos konfigūracija Pagr. būs. Joniz. en.(ev) 37 Rb Rubidis 85,4678 (Kr) 5s S 1/ 4, Sr Stroncis 87,6 (Kr) 5s 1 S 5, Y Itris 88,9585 (Kr) 4d 5s D 3/ 6,173 4 Zr Cirkonis 91,4 (Kr) 4d 5s 3 F 6, Nb Niobis 9,9638 (Kr) 4d 4 5s 6 D 1/ 6, Mo Molibdenas 95,94 (Kr) 4d 5 5s 7 S 3 7,94 43 Tc Technecis (98) (Kr) 4d 5 5s 6 S 5/ 7,8 44 Ru Rutenis 11,7 (Kr) 4d 7 5s 5 F 5 7, Rh Rodis 1,955 (Kr) 4d 8 5s 4 F 9/ 7, Pd Paladis 16,4 (Kr) 4d 1 1 S 8, Ag Sidabras 17,868 (Kr) 4d 1 5s S 1/ 7, Cd Kadmis 11,411 (Kr) 4d 1 5s 1 S 8,9938 P e r e i n a m i e j i e l e m en t a i 49 In Indis 114,818 (Kr) 4d 1 5s 5p P 1/ 5, Sn Alavas 118,71 (Kr) 4d 1 5s 5p 3 P 7, Sb Stibis 11,76 (Kr) 4d 1 5s 5p 3 4 S 3/ 8,684 5 Te Telūras 17,6 (Kr) 4d 1 5s 5p 4 3 P 9,96 53 I Jodas 16,945 (Kr) 4d 1 5s 5p 5 P 3/ 1, Xe Ksenonas 131,93 (Kr) 4d 1 5s 5p 6 1 S 1, Cs Cezis 13,955 (Xe) 6s S 1/ 3, Ba Baris 137,37 (Xe) 6s 1 S 5, La Lantanas 138,955 (Xe) 5d 6s D 3/ 5, Ce Ceris 14,116 (Xe) 4f 5d 6s 1 G 4 5, Pr Prazeodimis 14,977 (Xe) 4f 3 6s 4 I 9/ 5,473 L 6 Nd Neodimis 144,4 (Xe) 4f 4 6s 5 I 4 5,55 a 61 Pm Prometis (145) (Xe) 4f 5 6s 6 H 5/ 5,58 n 6 Sm Samaris 15,36 (Xe) 4f 6 6s 7 F 5,6437 t 63 Eu Europis 151,964 (Xe) 4f 7 6s 8 S 7/ 5,674 a 64 Gd Gadolinis 157,5 (Xe) 4f 7 5d 6s 9 D 6,1498 n 65 Tb Terbis 158,953 (Xe) 4f 9 6s 6 H 15/ 5,8638 o 66 Dy Disprozis 16,5 (Xe) 4f 1 6s 5 I 8 5,9389 i 67 Ho Holmis 164,933 (Xe) 4f 11 6s 4 I 15/ 6,15 d 68 Er Erbis 167,59 (Xe) 4f 1 6s 3 H 6 6,177 a 69 Tm Tulis 168,934 (Xe) 4f 13 6s F 7/ 6,1843 i 7 Yb Iterbis 173,4 (Xe) 4f 14 6s 1 S 6,54 71 Lu Lutecis 174,967 (Xe) 4f 14 5d 6s D 3/ 5,459 13
14 Z Elementas A Pagrindinės būsenos konfigūracija Pagr. Joniz. būs. en.(ev) 7 Hf Hafnis 178,49 (Xe) 4f 14 5d 6s 3 F 6, Ta Tantalas 18,9479 (Xe) 4f 5d s F 3/ 4 7, W Volframas 183,84 (Xe) 4f 14 5d 4 6s 5 D 7, Re Renis 186,7 (Xe) 4f 14 5d 5 6s 6 S 5/ 7, Os Osmis 19,3 (Xe) 4f 14 5d 6 6s 5 D 4 8, Ir Iridis 19,17 (Xe) 4f 14 5d 7 6s 4 F 9/ 8, Pt Platina 195,78 (Xe) 4f 14 5d 9 6s 3 D 3 8, Au Auksas 196,9666 (Xe) 4f 14 5d 1 6s S 1/ 9,55 8 Hg Gyvsidabris,59 (Xe) 4f 14 5d 1 6s 1 S 1,4375 P er e i n a m ie j i e l e m en t a i 81 Tl Talis 4,3833 (Xe) 4f 14 5d 1 6s 6p P 1/ 6,18 8 Pb Švinas 7, (Xe) 4f 14 5d 1 6s 6p 3 P 7, Bi Bismutas 8,984 (Xe) 4f 14 5d 1 6s 6p 3 4 S 3/ 7, Po Polonis (9) (Xe) 4f 14 5d 1 6s 6p 4 3 P 8, At Astatinas (1) (Xe) 4f 14 5d 1 6s 6p 5 P 3/ 86 Rn Radonas () (Xe) 4f 14 5d 1 6s 6p 6 1 S 1, Fr Francis (3) (Rn) 7s S 1/ 4,77 88 Ra Radis (6) (Rn) 7s 1 S 5, Ac Aktinis (7) (Rn) 6d 7s D 3/ 5,17 9 Th Toris 3,381 (Rn) 6d 7s 3 F 6, Pa Protaktinis 31,359 (Rn) 5f 6d 7s 4 K 11/ 5,89 A 9 U Uranas 38,89 (Rn) 5f 3 6d 7s 5 L 6 6,1941 k 93 Np Neptūnis (37) (Rn) 5f 4 6d 7s 6 L 11/ 6,657 t 94 Pu Plutonis (44) (Rn) 5f 6 7s 7 F 6,6 i 95 Am Americis (43) (Rn) 5f 7 7s 8 S 7/ 5,9738 n 96 Cm Kiuris (47) (Rn) 5f 7 6d 7s 9 D 5,9914 o 97 Bk Berklis (47) (Rn) 5f 9 7s 6 H 15/ 6,1979 i 98 Cf Kalifornis (51) (Rn) 5f 1 7s 5 I 8 6,817 d 99 Es Einšteinis (5) (Rn) 5f 11 7s 4 I 15/ 6,4 a 1 Fm Fermis (57) (Rn) 5f 1 7s 3 H 6 6,5 i 11 Md Mendelevis (58) (Rn) 5f 13 7s F 7/ 6,58 1 No Nobelis (59) (Rn) 5f 14 7s 1 S 6,65 13 Lr Lourensis (6) (Rn) 5f 14 7s 7p? P 1/? 4,9? 14 Rf Rezerfordis (61) (Rn) 5f 14 6d 7s? 3 F? 6,? Pastabos: 1. Ištisinės horizontalios linijos skiria elementų sistemos periodus.. Brūkšninės linijos atskiria elementus, kuriuose užpildomas priešpaskutinis arba trečiasis nuo galo elektronų sluoksnis (išskyrus kelias išimtis). Tai yra: (a) pereinamieji elementai (užpildomas priešpaskutinio sluoksnio d posluoksnis), (b) lantanoidai ir aktinoidai (užpildomas trečiojo nuo galo sluoksnio f posluoksnis). 3. Užrašymas, pvz., (Ar) 3d 6 4s reiškia elektronų konfigūraciją, kuri gaunama papildžius argono konfigūraciją šešiais 3d elektronais ir dviem 4s elektronais. 14
15 Nukleonų sluoksniai branduolyje Nukleonų sluoksniai tai artimų lygmenų grupės branduolio nukleono energijos lygmenų diagramoje. Branduoliai su pilnai užpildytu neutronų arba protonų sluoksniu yra ypač stabilūs. Istoriškai atitinkamos neutronų arba protonų skaičiaus vertės buvo pavadintos magiškaisiais skaičiais :, 8,, 8, 5, 8, 16. Magiškieji branduoliai. Branduoliai, kuriuose magiškieji yra ir protonų, ir neutronų skaičiai, vadinami dukart magiškaisiais: 4 He, 16 8 O, Ca, Ca, Pb. 8 Palyginimui elektronų skaičiai atomuose su pilnai užpildytais sluoksniais pagal idealiąją atomo sluoksnių užpildymo tvarką:, 1, 8, 6, 11, Elektronų skaičiai inertinių dujų atomuose:, 1, 18, 36, 54, 86. Sferinės begalinio gylio potencialo duobės modelis teisingai numato tik tris mažiausius magiškuosius skaičius (, 8, ). Tikslesnė nukleono potencinės energijos išraiška: U Ur () UKul() r r R 1 exp a Tačiau ir toks modelis teisingai numato tik tris mažiausius magiškuosius skaičius. U U(r) -U R r r Nukleono potencinė energija branduolyje 15
16 Branduolio modelis, kuris teisingai numato visus magiškuosius skaičius ir kai kurias kitas pagrindines branduolio savybes, gaunamas, pridėjus prie U(r) sukinio ir orbitos sąveikos energiją Eso UsoLs L Čia U so <. Galimas E so vertes lemia galimos L s L vertės. Jas galima gauti remiantis tuo, kad L L L Pakėlus kvadratu: j j s s L L L L L T. y. 1 ( h L Ls Lj L Ls ) [ j ( j 1) l ( l 1) s ( s 1)] Kadangi s = 1/, o j = l 1/, tai 1 1 lh, kai j l ; L Ls 1 1 ( l 1) h, kai j l. Atitinkamai 1 h l, kai j l ; Eso Uso 1 l 1, kai j l. Intervalas tarp dviejų polygmenių, į kuriuos skyla kiekvienas lygmuo su nenuliniu l dėl sukinio ir orbitos sąveikos: 1 Eso Uso h ( l 1) s 16
17 Nukleono energijos lygmenų diagramos, apskaičiuotos skirtingo pavidalo nukleono potencinėms energijoms, taikant sluoksninį branduolio modelį. Kairioji diagrama atitinka sferinę begalinio gylio potencialo duobę, vidurinioji diagrama atitinka realistišką potencinės energijos priklausomybę nuo radialiosios koordinatės, tačiau be sukinio ir orbitos sąveikos, o dešinioji diagrama gauta atsižvelgus į sukinio ir orbitos sąveiką 17
18 Radioaktyvumo sąvoka. Pagrindinis radioaktyviojo skilimo dėsnis Radioaktyvumas branduolių savaiminis virtimas kitų nuklidų branduoliais ( skilimas ). Protonų ir neutronų skaičiai, kurie atitinka stabiliuosius branduolius (juodos sritys) ir radioaktyviuosius branduolius (pilkos sritys) Pagal spinduliuojamų dalelių rūšį skiriami alfa () skilimas, beta () skilimas ir savaiminis dalijimasis. Kartu su kiekvienu iš šių trijų skilimo vyksmų dažnai atsiranda elektromagnetinė gama () spinduliuotė. Šios spinduliuotės kvantai (didelės energijos fotonai) vadinami gama () kvantais. Radioaktyviųjų branduolių skaičiaus priklausomybė nuo laiko ( radioaktyviojo skilimo dėsnis ): dn N ; dt čia N radioaktyviojo nuklido branduolių skaičius, o radioaktyviojo nuklido skilimo konstanta, rodanti, kuri branduolių dalis suskyla per laiko vienetą. yra skilimo tikimybė per laiko vienetą. Sprendinys yra eksponentinė laiko funkcija: / 1/ () e t Nt N N tt. Čia N yra radioaktyviojo nuklido branduolių skaičius pradiniu laiko momentu t =, o T 1/ yra radioaktyviojo nuklido pusėjimo trukmė (senesnis terminas pusamžis): ln T1/. Tai yra laikas, per kurį skyla pusė branduolių. Vidutinė gyvavimo trukmė tai vidutinis laikas iki branduolio skilimo: 1. Urano izotopo 38 9 U pusamžis lygus 4,519 m., radžio izotopo 6 88Ra 159 m., radono 86Rn 3,8 dienos, polonio Po 1,614 s. Radioaktyviojo šaltinio aktyvumas: dn. dt 18
19 N ln N N N(t) = N exp(t) = N t/t 1/ ln(n ) ln(n e t ) = ln(n ) t t (a) (b) Radioaktyviojo nuklido kiekio (a) ir jo logaritmo (b) priklausomybė nuo laiko t Aktyvumo vienetai: bekerelis (Bq): 1 Bq = 1 skil./s; kiuris (Ci; 1 Ci = 3,71 1 Bq), rezerfordas (Rd; 1 Rd = 1 6 Bq). = N. Šaltinio aktyvumo priklausomybės nuo laiko grafikas vadinamas skilimo kreive. / 1/ () () e t t N t N e t tt ; čia yra pradinis šaltinio aktyvumas: N. Tai reiškia, kad matuojant medžiagos aktyvumą galima nustatyti radioaktyvios medžiagos kiekį N. Aktyvumas matuojamas skaičiuojant išlėkusias daleles. Dalelių skaičiaus skirstinys Dalelių skaičius yra atsitiktinis. Todėl aktyvumą galima nustatyti tik apytiksliai. Santykinė paklaida didėja mažėjant detektuotų dalelių skaičiui. 8 8 Detektuotų per 1 s dalelių skaičius Detektuotų per 1 s dalelių skaičius Laikas (s) Laikas (s) Radioaktyviojo šaltinio spinduliuojamų dalelių skaičiavimo rezultatų pavyzdys. Vidurkis lygus 5 s 1 Radioaktyviojo šaltinio spinduliuojamų dalelių skaičiavimo rezultatų pavyzdys. Vidurkis lygus 5 s 1 Matavimų tikslas dalelių skaičiaus statistinio vidurkio nustatymas. Per fiksuotą laiką skilusių branduolių skaičius yra pasiskirstęs pagal Puasono skirstinį: x a a Px ( ) e (x =, 1,, ), x! čia P(x) yra tikimybė, kad per duotą laiką skils x branduolių, o a yra vidutinis per tą laiką skylančių branduolių skaičius. Puasono skirstinio atveju standartinis nuokrypis lygus šakniai iš vidurkio: x a. Jeigu a >, Puasono skirstinį galima aproksimuoti Gauso skirstiniu. Tada P( x a > x ) =.3, P( x a > x ) =.5. 19
20 Siekiant nustatyti atskirų dalelių skaičiaus matavimų rezultatų svyravimų statistinį reikšmingumą, reikia tuos svyravimus lyginti su kvadratine šaknimi iš tų pačių rezultatų. Dalelių skaičiaus neapibrėžtumą susitarta tapatinti su dvigubu standartiniu nuokrypiu N t (s) Radioaktyviojo skilimo metu kas 1 s detektuotų dalelių skaičiaus matavimo duomenys. Detektuojamų dalelių skaičiaus skirstinys priklauso nuo detektoriaus neveikos trukmės ( atsistatymo laiko ). Standartinio nuokrypio išraiška, įskaičius neveikos trukmės įtaką: n a1a T, čia T yra vieno matavimo trukmė, o n yra neveikos trukmė. Tuo remiasi vienas iš neveikos trukmės matavimo metodų: T e n 1, a e a e čia a e ir e yra empiriniai (išmatuotieji) vidurkis ir standartinis nuokrypis. Empirinio vidurkio standartinis nuokrypis: x a, n čia n yra matavimų skaičius. Todėl Puasono skirstinio atveju a a. n Empirinį rezultatų skirstinį nusako rezultatų histograma. Tai yra stulpelių diagrama, kurioje kiekvieno stulpelio kraštai nusako tam tikrą atsitiktinio dydžio verčių intervalą, o stulpelio aukštis lygus matavimų skaičiui, kurių metu išmatuotoji atsitiktinio dydžio vertė pakliuvo į tą intervalą. Kiekvieno histogramos stulpelio aukštis turi tam tikrą atsitiktinę komponentę. Standartinė paklaida: n n, n n i i i 1. n i i
21 Užregistruotų per 1 s dalelių skaičius Laikas (s) Histogramos sudarymas atlikus 1 matavimų, kurių kiekvieno trukmė 1 s Verčių pasikartojimų skaičius , Užregistruotų per 1 s dalelių skaičius Galutinė histograma, kuri atitinka aukščiau pateiktus duomenis Matavimų skaičius ,3,5,,15,1, Verčių pasikartojimų dažnis 6,8,7,6 P,5,4,3,,1, ((a x ) ) xa (a x ) ) x Puasono skirstinio pavidalas, kai vidurkis a yra didelis (a = 7,5). yra standartinis nuokrypis 1
22 Alfa skilimas dalelės tai 4 He branduoliai. A A4 4 ZX ZY He Ra 86Rn He. Pagrindinės skilimo ypatybės: 1) skilimas yra būdingas branduoliams, kurių Z > 8; ) kiekvienas radioaktyvus nuklidas spinduliuoja kelių tiksliai apibrėžtų energijų daleles; 3) dalelių kinetinės energijos priklauso palyginti siauram intervalui: E = (48,7) MeV; 4) Pusėjimo trukmė T 1/ sparčiai mažėja didėjant dalelių energijai E: D lgt1/ C. E Tai yra Geigerio ir Netolo dėsniu. Jeigu E išreikšta MeV, o T 1/ išreikštas s, tada C 5, D 13. Pirmąją ypatybę lemia tai, kad skilimas susijęs su nukleonų Kulono stūma. Išlekia būtent dalelė, nes tai yra ypač stabilus darinys (didelė savitoji ryšio energija). Branduolio ryšio energija E R yra priešinga pilnutinei branduolio nukleonų mechaninei energijai. ER [ Zmp ( A Z) mn M ] c, čia m p ir m n yra atitinkamai protono ir neutrono masės. Masės defektas : m E R / c. Savitoji ryšio energija: ER δer. A Išsiskyrusi energija įvairiems 3 U branduolio skilimo tipams: Emituota dalelė n 1 H H 3 H 3 He Išsiskyrusi energija (MeV) 7,6 6,1 1,7 1,4 9,9 Emituota dalelė 4 He 5 He 6 He 6 Li 7 Li Išsiskyrusi energija (MeV) +5,41,59 6,19 3,79 1,94 A ( E ) 1 ( E 1 ) 1 B ( E ) 3 B 1 dalelių greičių pasiskirstymo aiškinimas. Antrinis branduolys po alfa skilimo gali atsidurti įvairiuose energijos lygmenyse. Žemiausias energijos lygmuo vadinamas pagrindiniu, o aukštesnieji lygmenys vadinami sužadintaisiais.. B
23 E R / MeV () Savitosios ryšio energijos priklausomybė nuo branduolio masės skaičiaus A A lg T1/ (s) Kai kurių branduolių alfa skilimo pusamžio logaritmo priklausomybė nuo alfa dalelių energijos. Linijos atitinka izotopų sekas. Horizontaliosios ašies mastelis proporcingas 1/E 1/ Sunkiųjų elektringųjų dalelių sąveika su medžiaga Sunkiosios elektringosios dalelės tai atomų branduoliai ir jonai. Jų energija medžiagoje mažėja dėl elektrostatinės sąveikos su elektronais ir branduoliais (daugiausia su elektronais). 3
24 Didžiausias galimas nereliatyvistinės dalelės, kurios kinetinė energija E, o masė M, kinetinės energijos sumažėjimas dėl susidūrimo su nejudančiu elektronu, kurio masė m: 4me Emax E mev, M čia v yra krintančiosios dalelės greitis. Pvz., jeigu krintančioji dalelė yra 4 MeV energijos dalelė, tada E max, kev << E. Todėl sunkioji dalelė juda beveik tiesiai viso lėtėjimo metu. Dalelės siekis (trajektorijos ilgis) šiuo atveju beveik sutampa su įsiskverbimo gyliu (jeigu kritimo kampas yra 9). Delta spinduliai tai palyginti mažos energijos antriniai elektronai, kuriuos dalelė išlaisvino iš atomų. Jie irgi gali jonizuoti kitus atomus. Betės formulė de / dx tai ilginė stabdymo geba. Jos išraiškos išvedimas: Sąveikos su nejudančiu elektronu jėgos modulis: 1 ze F 4π x b Sąveikos metu elektronui perduotas pilnutinis judesio kiekis yra lygus p F dt. Lygiagrečiosios komponentės integralas laiko atžvilgiu lygus nuliui: F dt. Judesio kiekis, kurį gauna elektronas, yra statmenas krintančiosios trajektorijai ir lygus 1 1 ze p Fdt Fdx v π bv. Energija, kurią gavo medžiagos elektronas: 4 p 1 ze E. me 8π mev b Jonizacinė ilginė stabdymo geba yra lygi integralui Todėl bmax de p 1 bmin 4 e nπbdb e mev z e n b ln dx m 4π b b b b ~ 1 E. max max ln ln ln min E E min 1 E E max min. max min E min = I (vidutinė jonizacijos energija). b ln b max min 1 ln mev. I 4 de 1 z e n mev ln. dx 8π mev I Tikslesnė išraiška (Betės formulė): 4 de 1 z e n mev ln, dx 4π mev I(1 ) v / c. Elektronų koncentracija: Z N n A, A. ; Atomo jonizavimo sunkiosios elektringosios dalelės elektriniu lauku klasikinis modelis. ze krintančiosios dalelės krūvis, e atomo elektrono krūvis ze ze F v F db -e b x= Tūrio elementas integruojant dalelės energijos nuostolius sluoksnio tūriu dx b dalelės 4
25 Z yra medžiagos, kuri stabdo dalelę, vidutinis atominis numeris, yra medžiagos tankis, N A yra Avogadro skaičius, o A yra medžiagos molinė masė (t. y. atominis masės skaičius). I 11 Z ev. Pvz., oro I = 86 ev. Masinė stabdymo geba de/( dx) nepriklauso nuo medžiagos tankio (priklauso tik nuo medžiagos cheminės sudėties). Masinis siekis tai masė ploto vienetui: R R. R' silpnai priklauso nuo medžiagos cheminės sudėties (t. y. R ~ 1 / ). Todėl 1 R R1. Beta skilimas Branduoliai, kurie turi neutronų perteklių, dažniausiai skyla išspinduliuodami elektroną. Branduoliai, kurie turi protonų perteklių, dažniausiai skyla išspinduliuodami pozitroną arba pagaudami vieną iš atomo vidinių sluoksnių elektronų. Toks skilimas vadinamas beta skilimu. dalelių (elektronų arba pozitronų) energijos spektras yra tolydus. Dešinysis spektro kraštas yra ties energija (M 1 M m e )c, čia M 1 yra pirminio branduolio rimties masė, M yra antrinio branduolio masė, o m e yra elektrono rimties masė. Tačiau vidutinė elektronų energija yra lygi tik maždaug trečdaliui didžiausios energijos. Taip yra dėl to, kad dalį išsiskyrusios energijos nusineša dar viena dalelė, kuri išlekia skilimo metu (neutrinas arba antineutrinas). Elektronų, kuriuos emituoja bismuto izotopas 1 83 Bi, kinetinės energijos pasiskirstymas Beta skilimo metu vienas branduolio neutronas virsta protonu arba atvirkščiai: n p e, p n e Elektrono pagavimas ( K pagavimas ): p e n. 5
26 3 + Na (,6 m.) +,545 MeV (89,84 %) + 1,8 MeV (,6 %) + 1,746 MeV Elektrono pagavimas (1,1 %) + Ne Natrio izotopo Na beta skilimo schema. Schemoje parodyti pusamžis, didžiausios dalelių energijos, atitinkamų skilimų tikimybės ir kvantinis šuolis tarp Ne lygmenų Elektronų sąveika su medžiaga Kaip ir sunkiosios elektringosios dalelės, elektronai medžiagoje praranda energiją dėl elektrostatinės sąveikos su medžiagos atomų elektronais. Dėl susidūrimų su medžiagos elektronais ir branduoliais elektronų judėjimo trajektorija medžiagoje yra netaisyklingos formos (kitaip negu sunkiųjų dalelių, kurių trajektorijos yra tiesios). Atsižvelgus į kvantinius pakaitinius efektus, gaunama šitokia elektronų jonizacinės ilginės stabdymo gebos išraiška: 1 en 1 mev E E S jon ln 1 1 ln 1 1 4π mev I mec 16 Čia E yra elektrono reliatyvistinė kinetinė energija: mc e E mc e. 1 4 Sunkiųjų dalelių ir elektronų jonizacinės ilginės stabdymo gebos išraiškos skiriasi tik daugikliu riestiniuose skliaustuose, kuris silpnai priklauso nuo dalelės greičio v ir nuo atomo vidutinės sužadinimo energijos I. Krintantysis elektronas, kuloniškai sąveikaudamas su medžiagos elektronais ir branduoliais, dėl savo mažos masės gali įgyti didelį pagreitį. Su pagreičiu judantis krūvininkas spinduliuoja elektromagnetines bangas (stabdomoji spinduliuotė). Tai yra dar vienas energijos nuostolių mechanizmas. Atitinkama ilginė stabdymo geba vadinama radiacine ilgine stabdymo geba: e Z( Emc e ) n ( Emc e ) 4 Srad 4ln 4 ; 4π 137mc e mc e 3 Srad EZ. S jon 16mc e S rad > S jon, jeigu E > 8 / Z MeV. β Lygiagretaus elektronų pluošto sklaida medžiagoje. 6
27 N N Dalelių siekio matavimas. Energijos apskaičiavimas pagal siekį lnn lnn lnn' N / Tipiška vienos energijos dalelių srauto priklausomybė nuo sugėriklio storio d. R ir R max yra vidutinis ir didžiausias siekiai R R max d ln(fonas) (b) Tipiška elektronų, kuriuos spinduliuoja radioaktyvusis šaltinis, sugerties kreivė naudojant logaritminę ordinačių ašies skalę. R e ekstrapoliuotasis siekis. R e R d Jeigu elektronus spinduliuoja beta radioaktyvi medžiaga, tada sugerties kreivėje yra eksponentinė sritis: N( d) N exp( d). vadinamas silpimo koeficientu. Siekio ir stabdymo gebos sąryšis: E de R d E /dx Tačiau praktikoje patogiau naudotis įvairiomis empirinėmis formulėmis. Pvz., dalelių, kurių energija yra tarp 4,5 MeV ir 8 MeV, siekį ore galima apskaičiuoti pagal formulę 3/ R 3,18E, čia R išreikštas mm, o E išreikštas MeV. dalelių, kurias spinduliuoja radioaktyvieji nuklidai, didžiausios energijos E max matavimui galima panaudoti empirinį sąryšį tarp masinio siekio ir didžiausios energijos E max :,11( 1, 4 E 1) ; Rm čia E max išreikšta MeV, o R m išreikštas g/cm. Ši apytikslė lygybė galioja, kai dalelių didžiausia energija priklauso intervalui < E max < 3 MeV. Skilimų grandinės. Radioaktyvioji pusiausvyra A B C... At NA( t) NA()e. dnb BNB ANA. dt B Padauginus abi lygybės puses iš e t : d ( B B B e t ) A A e t N N. dt d ( B ( B A) B e t ) A A ()e t N N. dt Bt ( B A) t A ( B A) t NBe ANA() e d t NA()e K, B A čia K yra integravimo konstanta. Jeigu N B () = A K NA (). B A A At Bt NB() t NA()(e e ). B A Jeigu B << A, Bt N ( t) N ()e. B A max 7
28 A B Jeigu A < B, tada po pakankamai ilgo laiko (kad galiotų nelygybė e >>e ) A At A NB( t) NA()e NA( t). B A B A Tai yra radioaktyvioji pusiausvyra: abiejų nuklidų kiekių santykis yra pastovus ir lygus NB A, N A B A ir abiejų nuklidų kiekiai mažėja su pirminio nuklido skilimo konstanta. Jeigu A << B, tada NB A TB 1, NA B TA t. y. A N A B N B (abiejų nuklidų aktyvumai yra vienodi). Jeigu A << B ir A << C, tada pusiausvyros sąlygomis NC B TC. NB C TB Šis santykis gali būti ir didesnis už 1, ir mažesnis. t t Pagrindiniai nuklidai, kurie priklauso 6 Ra skilimo grandinei Nuklidas Skilimo tipas Skilimo pusamžis dalelių energija (MeV) 6 Ra 16 m. 4,78 Rn 3,85 d. 5,49 18 Po 3,5 min 6, 14 Pb β 6,8 min 14 Bi β 19,7 min 14 Po 1,6 1 4 s 7,68 1 Pb β m. 1 Bi β 5,1 d. 1 Po 138,4 d. 5,3 6 Pb Stabilus 8
29 Gama spinduliavimas Gama () spinduliuotė tai elektromagnetinės bangos, kurių bangos ilgis yra daug mažesnis už 1 1 m (1 Å). Kvantinės mechanikos požiūriu tai yra dalelių fotonų arba gama kvantų srautas. spinduliuotės diapazonas iš dalies persikloja su rentgeno spinduliuotės diapazonu. Branduolių spinduliuotė atsiranda dėl sužadintojo branduolio kvantinių šuolių į žemesnius energijos lygmenis. Fotono energija lygi h Ea Eb. Ypač ilgaamžės sužadintosios būsenos vadinamos metastabiliosiomis būsenomis. Energijos perteklių branduolys gali prarasti ne vien emituodamas fotoną, bet ir perduodamas jį vienam iš atomo elektonų (vidinė konversija) arba susidarant elektono ir pozitrono porai (vidinis porų kūrimas). Vidinės konversijos elektrono energija: E e = E r. Vidinis porų kūrimas galimas tik tada kai sužadinimo energija yra didesnė už mc = 1,MeV. spinduliuotė gali atsirasti ir vykstant vadinamajai anihiliacijos reakcijai. Žemės sąlygomis lengviausia realizuoti elektrono ir pozitrono anihiliaciją. Jos metu priešingomis kryptimis išspinduliuojami du fotonai, kurių kiekvieno energija lygi elektrono rimties energijai m e c = 511 kev. 57 Co Elektrono pagavimas T 1/ =71,4 d. Gama spinduliuotės sąveika su medžiaga 5/ 3/ 1/ 136,4 9% 1 kev 91% 57 Fe 11 T 1/ =1 s 7 T 1/ =1 s 14,4 kev Radioaktyviojo skilimo 57 Co 57 Fe schema. Kiekvieno lygmens kairėje nurodytas branduolio sukinio kvantinis skaičius. Viršutinis indeksas šalia to skaičiaus nusako būsenos lyginumą ( reiškia lyginę banginę funkciją, o reiškia nelyginę banginę funkciją) Sąveikos skerspjūvio sąvoka Sąveikos skerspjūvis tai įsivaizduojama plokščia sritis, kurios plotas parinktas taip, kad duotosios rūšies sąveikos (susidūrimo) tikimybė sutaptų su tikimybe, kad krintančioji dalelė pataikys į šią sritį. Priskyrus kiekvienam taikinio sluoksnio atomui skerspjūvį, pilnutinis atomų plotas ds', kuris uždengia dalį pilnutinio sliuoksnio ploto S, yra lygus skerspjūvių sumai, t. y. ds' = nsdx. Todėl geometrinė pataikymo į kurį nors vieną atomą tikimybė lygi ds dp ndx, S čia n yra atomų koncentracija. S dx Sąveikos skerspjūvio aiškinimas 9
30 Diferencialinis (kampinis) sąveikos skerspjūvis: = d/d, čia dyra skerpjūvis įvykio, kuris pasireiškia antrinės (pvz., išsklaidytos) dalelės išlėkimu į nykstamąjį erdvinį kampą d. x d r r d Antrinė dalelė Pilnutinis ( integralinis ) skerspjūvis: π π d d sind. Kadangi dažniausiai nepriklauso nuo azimutinio kampo, tai π π sind. z Krintančioji dalelė y w Diferencialinio sąveikos skerspjūvio apskaičiavimui Fotoelektrinis efektas Fotoefekto atveju visa fotono energija išeikvojama tam, kad išlaisvinti elektroną iš medžiagos atomo. Fotoelektono kinetinė energija yra lygi čia E r yra elektrono ryšio energija. T E E r, Atomas, kuris neteko vidinio elektrono, yra sužadintos būsenos. Sužadinimo energija gali būti perduota kitiems to atomo elektronams, kurie išlekia iš atomo: Ožė (pranc. Auger) reiškinys. Be to, į atsiradusią vakansiją gali pereiti aukštesnio sluoksnio elektronas. Šio kvantinio šuolio metu emituojamas fotonas (rentgeno fluorescencija). Fotoefekto skerspjūvio priklausomybėje nuo E yra trūkiai, kurie vadinami sugerties kraštais. Jie atsiranda todėl, kad fotoefektas yra galimas tik kai fotono energija yra didesnė už elektrono ryšio energija, kuri yra skirtinga skirtingiems elektronų sluoksniams. Paskutinis (didžiausios energijos) šuolis yra aukščiausias ( K kraštas ). Fotoefekto skerspjūvio priklausomybė nuo Z ir E, kai E yra 1 kev eilės: 5 Z ~. fe Komptono sklaida Komptono sklaidos atveju fotoną išsklaido elektronas (dažniausiai valentinis atomo elektronas). Sąveikos kinematika beveik tokia pati, lyg tas elektronas būtų laisvas. Šios sąveikos pasekmė yra mažesnės energijos E fotonas ir atatrankos elektronas, kurio kinetinė energija T lygi 3,5 E T E E E mc, čia E yra pilnutinė reliatyvistinė elektrono energija. p p Pakėlus kvadratu ir padauginus iš c : 4 ( pc) E ( E ) EE cos E m c, E E. 1 ( E / mc )(1 cos ) Kai E yra mc eilės arba didesnė, E (min) mc / 56 kev. Atominis Komptono sklaidos skerspjūvis yra lygus Z C, čia C yra elektroninis Komptono sklaidos skerspjūvis (jis priklauso tik nuo fotono energijos). 3
31 Atatrankos elektronas (a) Komptono sklaidos geometrija; (b) vektorinis sąryšis tarp trijų impulso vektorių Komptono sklaidos laisvaisiais elektronais diferencialinis skerspjūvis C (), apskaičiuotas pagal Kleino ir Nišinos formulę, kai E kinta nuo iki 5 MeV Porų kūrimas Porų kūrimo metu visa fotono energija išeikvojama kuriant elektrono ir pozitrono porą atomo elektriniame lauke. Energijos tvermės dėsnis: T T E mc. Porų kūrimas galimas tik tada, kai E > mc = 1, MeV. Sulėtėjus pozitronui medžiagoje, jis anihiliuoja, todėl atsiranda anihiliacinė spinduliuotė (,511 MeV). 31
32 Silpimo koeficientas Jeigu fotonų pluoštas yra gerai kolimuotas (t. y. jeigu jis yra siauras ir lygiagretus), tada pluošto intensyvumo sumažėjimas perėjus storio dx medžiagos sluoksnį yra lygus di N Idx. Gama spinduliuotės pluošto silpimo koeficiento matavimo metodika, kai pluoštas yra lygiagretus, t. y. kolimuotas (a), ir kai pluoštas yra nekolimuotas (b). S yra šaltinis, kurio skleidžiama spinduliuotė pereina per medžiagos sluoksnį ir pasiekia detektorių D. (a) atveju sklaida ir sugertis pasireiškia vienodai, nes mažina fotonų, kurie pataiko į detektorių D, skaičių. (b) atveju detektuojama daugiau fotonų, nes kai kurie fotonai išsklaidomi į detektorių. Todėl šiuo atveju eksperimentinė silpimo koeficiento vertė yra mažesnė už tikrąją Pilnutinis skerspjūvis yra lygus visų trijų sąveikos vyksmų skerspjūvių sumai: Z. fe C p I I exp( N x) I exp( x), yra ilginis silpimo koeficientas: N. Masinis silpimo koeficientas yra lygus ilginio silpimo koeficiento ir medžiagos tankio santykiui:. m / Fotonų masinio sugerties koeficiento aliuminyje ir švine priklausomybė nuo fotono energijos. Brūkšninės linijos rodo masinio sugerties koeficiento dėmenis, atitinkančius fotoelektrinę sugertį, Komptono sklaidą ir porų kūrimą 3
33 Branduolinės reakcijos Branduolinės reakcijos sąvoka Branduolinė reakcija (siaurąja prasme) tai bet koks branduolio virsmas dėl sąveikos su dalele. Palyginimui: radioaktyvusis skilimas yra savaiminis virsmas (nereikalaujantis išorinio poveikio). Branduolinės reakcijos užrašymas: axy b arba X (a, b) Y, čia a yra krintančioji dalelė, X yra taikinio branduolys (dažniausiai nejudantis), o Y ir b yra reakcijos produktai: Y yra sunkioji dalelė (atomo branduolys), o b yra lengvoji dalelė (pvz., kvantas arba nukleonas). Reakcijos energija (šiluma): Q( ma mx mb my) c Jeigu Q >, tada reakcija yra egzoterminė, o jeigu Q < endoterminė. Sąveikos skerspjūvis ir reakcijos sparta Branduolinių reakcijų skerspjūvius įprasta išreikšti barnais (1 b = 1 8 m ). Reakcijos sparta tai reakcijos įvykių skaičius per laiko vienetą. Tikimybė, kad viena krintančioji dalelė sukels reakciją: dp ndx. Tikimybė per laiko vienetą vienai dalelei: dp dx n nv, dt dt Reakcijos sparta tūryje V: nvnkr V Nv nkr N j ; čia n kr yra krintančiųjų dalelių koncentracija (skaičius tūrio vienetui), N = nv yra taikinio dalelių skaičius tūryje V, o j = vn kr yra krintančiųjų dalelių srauto tankis (dalelių skaičius ploto vienetui per laiko vienetą). Tarpinio branduolio reakcijos Tarpinio branduolio reakcija vyksta dviem etapais: 1. Krintančioji dalelė ir taikinys susilieja į vieną branduolį ( tarpinį branduolį).. Praėjus pakankamai dideliam laikui, kad nusistovėtų dinaminė pusiausvyra, tarpinis branduolys skyla. Tarpinio branduolio egzistavimo trukmė yra 1 18 s 1 16 s. Jo skilimas panašus į įkaitusio skysčio lašo garavimą, t. y. gali išlėkti nukleonas (panašiai kaip molekulė išlekia iš skysčio). Tačiau, jeigu tarpinio branduolio perteklinė (sužadinimo) energija nėra daug didesnė už nukleono ryšio energiją, tada labiau tikėtinas procesas, kurio metu iš branduolio išlekia fotonas (gama kvantas): spinduliuojamasis pagavimas. Reakcijos skerspjūvis (b) 6 Li(n, )t Branduolinės reakcijos 6 Li(n,)t skerspjūvio priklausomybė nuo neutrono energijos. Ties 5 kev matomas rezonansas Neutrono energija 33
34 4.6. Dirbtinis radioaktyvumas Kadangi reakcijos skerspjūvis yra atvirkščiai proporcingas neutronų greičiui, neutronai yra lėtinami. Tam naudojamos medžiagos, kuriose daug vandenilio (pvz., vanduo, parafinas). Tokioje medžiagoje ( neutronų lėtiklyje ) neutronai lėtėja dėl tampriųjų susidūrimų su protonais. Neutronai dažniausiai gaunami vykdant (, n) tipo branduolinę reakciją Be He 6C n. Toks neutronų šaltinis tai mišinys metalinio berilio miltelių ir nedidelio kiekio radioaktyviosios medžiagos (pvz., plutonio izotopo 39 Pu). Pradinė neutrono energija nuo iki 13 MeV. Spinduliuojamojo neutrono pagavimo reakcija (n, ) yra naudojama gaminant radioaktyvias medžiagas. Šiluminio neutrono pagavimas yra tarpinio branduolio reakcija: A 1 A1 * A1 ZX n ZX ZX γ ( * reiškia sužadintą branduolį). Trumpesnis užrašymas: A 1 A1 ZX n ZX γ. Spinduliuojamojo neutrono pagavimo metu susidaręs nuklidas dažnai būna aktyvus. Pavyzdžiai branduolinės reakcijos, kuriose dalyvauja stabilieji sidabro izotopai Ag ir 47 Ag : Ag n 47Ag γ, Ag n 47Ag γ. Šių reakcijų metu susidarę nuklidai Ag ir 47 Ag yra radioaktyvūs: Ag 48Cd e νe 14s Ag 48Cd e νe 4,6s,. Gamtiniame sidabre yra 51,35 % Ag ir 48,65 % 47 Ag. Aktyvinimas tai radioaktyvios medžiagos gaminimas vykdant neutrono pagavimo reakciją. Antrinio nuklido (pvz., Ag ) kiekio didėjimo sparta aktyvinimo metu lygi dn Nbr j N ; dt čia yra antrinio nuklido skilimo konstanta (antrasis dėmuo atspindi antrinių branduolių skilimą). Didžiausiasis ( soties ) antrinio branduolių skaičius N s lygus Nbr j T1/ Ns Nbr j Nbr j. ln Čia ir T 1/ yra antrinio nuklido branduolių vidutinė gyvavimo trukmė ir pusamžis. Antrinio nuklido branduolių skaičiaus priklausomybė nuo aktyvinimo trukmės (t a ): ta ta / T1/ Nt ( a) Ns(1e ) Ns(1 ). Bandinio aktyvumas: ta ta / T1/ ( ta) N( ta) Ns(1e ) Ns(1 ). Soties aktyvumas: s = N s. Aktyvinimo pradžioje (kai t a << T 1/ ) N(t a ) = N br jt a. 34
35 s,938 s,875 s,75 s,5 s Aktyvacijos kreivė T 1/ T 1/ 3T 1/ 4T 1/ 5T 1/ t. t a aktyvinimo trukmė, bandinio aktyvumas, s a s (1 e ) soties aktyvumas, skilimo konstanta, T 1/ = ln/ pusamžis t a 35
36 Jonizuojančiosios spinduliuotės detektorių bendrosios savybės Supaprastintas detektoriaus modelis 1) spinduliuotė sukuria laisvuosius krūvininkus detektoriaus darbinėje medžiagoje; ) veikiami elektrinio lauke, kuris yra sukurtas detektoriuje, krūvininkai juda ir sukelia elektros srovę apkrovos grandinėje. t c itdt () Q. Čia t c yra krūvininkų surinkimo trukmė (laikas, per kurį krūvininkai pasiekia elektrodus). it () It () t c t Detektoriaus srovės impulsų pavyzdžiai. Punktyrinė linija nusako srovės laikinį vidurkį I(t) Detektoriaus impulsinė veika it () Detektorius C R Ut () Detektoriaus impulsinės veikos supaprastinta ekvivalentinė schema Bendroji impulso U(t) išraiška: t 1 t t Ut () it ( )exp dt C RC. Dažniausiai RC >> t c. Tada krūvio surinkimo metu (kol t < t c ) t 1 Ut ( ) it ( )d t ( t tc ) C. Todėl tokią detektoriaus veiką galima vadinti srovės integravimo veika. Praėjus laikui t c nuo sąveikos įvykio, matuojamas signalas yra lygus savo didžiausiai vertei Q Umax. C Paskui talpa C pradeda išsielektrinti per apkrovos varžą R, o įtampa mažėja eksponentiškai: t tc Ut () Umax exp tt c RC. 36
37 (a) i Q i( t) dt (a) Hipotetinio detektoriaus srovės impulsas. (b) Matuojama įtampa esant didelei apkrovos grandinės trukmės konstantai (b) U t c RC >> t c Umax = Q / C t dn dh Impulsų amplitudžių spektrai. Energinė skyra Diferencialinio impulsų amplitudžių spektro pavyzdys Impulsų su amplitudėmis nuo H 1 iki H skaičius: Pilnutinis impulsų skaičius N : H 1 H H 3 H 4 H 5 Impulso amplitudė H dn N( H1 H H) dh. dh N H1 dn d H. dh Norint amplitudžių spektrą paversti energijų spektru, reikia visų taškų abscises H pakeisti atitinkamomis energijomis E, o ordinates padauginti iš išvestinės dh/de. Jeigu spektras gautas, esant monoenerginei spinduliuotei, tada jis vadinamas atsako funkcija duotajai krintančiųjų dalelių energijai. Detektorių, kurie naudojami matuojant dalelių energiją, atsako funkcija yra apytiksliai Gauso funkcijos pavidalo, o vidutinės amplitudės H ir dalelių energijos E santykis yra konstanta: H const E. 37
38 dn dh Y Energinė skyra H R H (a).66y.5y H H H H dn de Y Energinė skyra E R E (b).66y.5y E E E E Detektoriaus energinės skyros apibrėžimas. (a) Amplitudinė atsako funkcija; (b) Energinė atsako funkcija. 38
39 Gama spektrometrijos fizikiniai pagrindai Antrinių elektronų energijos spektras (a) (b) (c) Po įvairių įvykių atsiradusių antrinių elektronų energijos spektrai. (a) Po fotoefekto; (b) po vienkartinės Komptono sklaidos; (c) po elektrono ir pozitrono poros kūrimo ir abiejų anihiliacinių fotonų nuotėkio. Fotoefekto atveju impulso amplitudė proporcinga fotoelektrono energijai: E f = hν ε r. Komptono sklaidos atveju amplitudė proporcinga Komptono atatrankos elektrono energijai: EK h h. h h ; 1 (1 cos ) (1 cos ) EK h ; 1 (1 cos ) čia h /( m c ). E K max mc 1 Porų kūrimo atveju impulso amplitudė proporcinga elektrono ir pozitrono kinetinių energijų sumai: E E h m c. h h. 39
40 Detektoriaus atsako funkcijos pavidalas Komptono sklaidos ir porų kūrimo atveju atsiranda antrinė gama spinduliuotė (atitinkamai išsklaidytoji ir anihiliacinė spinduliuotė). Šios spinduliuotės sąveika su detektoriaus darbine medžiaga turi įtakos detektoriaus atsako funkcijai. Išlekiantis išsklaidytasis fotonas (dalinė energijos sugertis) Komptono sklaida Fotoefektas Išlekiantys 511 kev anihiliacinės spinduliuotės fotonai γ kvanto energijos perdavos medžiagai sekų pavyzdžiai. (a) (b) γ spinduliuotės detektoriaus atsako funkcijos bendrasis pavidalas. (a) Atsako funkcija, kai antriniai elektronai atsiranda tik dėl Komptono sklaidos ir fotoefekto. (b) Atsako funkcija, kai kartu su Komptono sklaida ir fotoefektu vyksta ir elektrono-pozitrono porų kūrimas. 4
41 γ spektrometro pagrindinės dalys. Spektrometro kalibravimas Impulsų amplitudžių spektras matuojamas amplitudžių analizatoriumi, taip pat vadinamu daugiakanaliu analizatoriumi. Daugiakanalis analizatorius rūšiuoja impulsus pagal jų amplitudes. Kiekvienas užfiksuotas impulsas priskiriamas vienam iš kanalų. Kanalas tai impulsų amplitudžių intervalas. Matuojamas impulsų amplitudžių spektras amplitudės funkcija N/H, kur N yra kiekvieną kanalą atitinkantis impulsų skaičius, o H yra kanalo plotis. Amplitudės matavimo vienetą patogu pasirinkti lygų kanalo pločiui. Tada H = 1, N/H = N, o amplitudė H yra lygi kanalo numeriui. Taigi, amplitudžių spektras tai amplitudžių histograma. Detektorius γ šaltinis Priešstiprintuvis Stiprintuvas t H Daugiakanalis analizatorius arba kompiuteris Aukštos įtampos šaltinis Paprasčiausio γ spektrometro sandara. Priešstiprintuvio išėjimo impulsai dažniausiai turi trumpą (1-9 s eilės) priekinį frontą, ilgą ((5 1) 1-5 s trukmės) užpakalinį frontą ir maža amplitudę (kelių milivoltų eilės). Stiprintuvo išėjimo impulsai yra labiau simetriški, jų trukmė (Δt) yra 1-6 s eilės, o amplitudė (H) yra kelių voltų eilės. Spektrometru kalibravimu vadinamas funkcijos H(E) arba E(H) matavimas. Ši funkcija vadinama kalibravimo kreive. Idealiuoju atveju H ae. Tačiau realių spektrometrų kalibravimo kreivė yra netiesinė. Tą netiesiškumą galima įskaityti aproksimuojant kalibravimo kreivę laužte. Vienos atkarpos lygtis yra H ae b. Apytiksliam spektrometro kalibravimui reikia turėti bent dviejų skirtingų energijų (E 1 ir E ) γ spinduliuotės šaltinius, kurių spinduliuotės energija yra žinoma, arba vieną šaltinį, kuris spinduliuoja bent dviejų žinomų energijų fotonus. Vietoj dviejų skirtingų šaltinių gali būti naudojamas ir vienas γ šaltinis, kuris spinduliuoja bent dviejų žinomų diskrečių energijų γ kvantus. Tada H H1 a, E E1 b H1 ae1. H b E. a Tiksliausi rezultatai gaunami, kai E 1 < E < E. Amplitudžių spektruose (histogramose) stulpelių aukščiai pasiskirstę pagal Puasono skirstinį. T. y., jeigu stulpelio aukštis yra N, tada jo santykinis standartinis nuokrypis lygus N / N 1/ N. Vadinasi spektro tikslumas didėja augant dalelių skaičiams N. 41
42 4 N N N max N = N max = 19 N N N max max max Dalelių skaičius N Kanalo numeris H Amplitudžių spektras, kuris iškraipytas atsitiktinių fliuktuacijų. Pirmasis ir paskutinysis kanalai, kuriuos atitinkanti N N vertė priklauso intervalui [ Nmax Nmax, Nmax Nmax ], yra Nr. 39 ir Nr. 61. Todėl galima teigti, kad maksimumą atitinkančio kanalo numeris yra ( ) / = 5, o jo neapibrėžtumas (atsitiktinė paklaida) yra apytiksliai lygus (61 39) / = 11. 4
43 Dviejų nukleonų sąveikos potencinė energija Stūma Trauka Branduolio ryšio energija Branduolinės jėgos savybės Kadangi branduolinei jėgai yra būdina soties savybė, tai branduolys yra apytiksliai rutulio formos; jo spindulys lygus 1/3 R RA R 1,1 15 m. ; Branduolinės jėgos savybės: 1. Branduolinė trauka tarp nukleonų yra artisiekė, t. y. ji pasireiškia tik tada, kai atstumas tarp nukleonų yra labai mažas (1 15 m eilės).. Branduolinė jėga nėra vien tik traukos jėga: ji turi ir stūmos komponentę, kuri pradeda vyrauti, kai atstumas tarp nukleonų sumažėja iki maždaug, m. Todėl egzistuoja tam tikras pusiausvirasis atstumas tarp gretimų nukleonų. Su tuo susijusi branduolinės jėgos soties savybė: kiekvieno nukleono (išskyrus branduolio paviršiuje esančius nukleonus) potencinė energija dėl sąveikos su kitais jį supančiai nukleonais yra apytiksliai vienoda visuose branduoliuose. Vienas iš šios soties požymių apytikslis branduolio medžiagos tankio pastovumas. Branduolio spindulys: 1/3 R R A ; R 1,1 15 m. r Atstumas Dviejų nukleonų sąveikos potencinės energijos priklausomybė nuo atstumo tarp jų 3. Branduolinei jėgai yra būdinga krūvinė simetrija, t. y. dviejų duotos būsenos neutronų branduolinės sąveikos jėga yra tiksliai lygi dviejų tokių pačių būsenų protonų branduolinės sąveikos jėgai. Neutrono ir protono branduolinės sąveikos jėga nežymiai skiriasi nuo dviejų vienodų nukleonų sąveikos jėgos. 4. Branduolinė jėga priklauso nuo kampo tarp nukleonų sukinių. Sukinys tai vidinis dalelės (nukleono) judesio kiekio momentas. Empiriškai nustatyta, kad neutrono ir protono sukinių kryptys surištojoje neutrono ir protono sistemoje deuterio branduolyje (deutone) yra vienodos. Tai rodo, kad dviejų vienodos sukinio krypties nukleonų vidutinė traukos jėga yra stipresnė už dviejų priešingų sukinio krypčių nukleonų sąveikos jėgą. Iš Paulio draudimo principo išplaukia, kad vienodų nukleonų kvantinės būsenos turi būti skirtingos. Tai reiškia, kad dviejų vienodos erdvinio judėjimo būsenos neutronų arba dviejų protonų sukinių kryptys turi būti priešingos. Dviejų vienodos erdvinio judėjimo būsenos skirtingų nukleonų (neutrono ir protono) sukinių kryptys gali būti ir vienodos, ir priešingos, nes Paulio draudimo principas galioja tik tada, kai dalelės yra vienodos. Todėl, atsižvelgus į pirmiau 43
44 minėtą dviejų nukleonų traukos jėgos priklausomybę nuo kampo tarp jų sukinių, gaunama, kad vidutinė neutrono ir protono traukos jėga branduolyje yra didesnė negu vidutinė dviejų neutronų arba dviejų protonų traukos jėga. Šios dvi jėgos skiriasi maždaug du kartus. 5. Dviejų nukleonų branduolinės sąveikos jėga priklauso nuo kampo tarp abiejų nukleonų pilnutinio sukinio vektoriaus L S ir jų reliatyviojo judėjimo judesio kiekio momento vektoriaus L. Jėgos komponentė, kuri nusako šią priklausomybę, yra vadinama sukinio ir orbitos sąveikos jėga. Ji yra proporcinga skaliarinei sandaugai L L S. Branduolio ryšio energija ir Veiczekerio formulė Savitoji ryšio energija tai vidutinė ryšio energija vienam nukleonui: ER δ ER. A E R / MeV Veiczekerio formulė: /3 1/3 1 ER AA Z( Z 1) A ( N Z) A C = 15,5 MeV, = 16,8 MeV, =,7 MeV, = 3 MeV, jeigu Z ir N lyginiai, C jeigu A nelyginis, 34 MeV. 3/4 jeigu Z ir N nelyginiai; A () Savitosios ryšio energijos priklausomybė nuo branduolio masės skaičiaus A A 44
45 1) Pirmasis dėmuo nusako ryšio energijos dalį, kurią lemia įsotinti ryšiai tarp nukleonų, t. y. vidinių branduolio nukleonų branduolinės traukos jėgos. ) Antrasis dėmuo atspindi paviršinius efektus, t. y. neįsotintus paviršinių nukleonų ryšius. 3) Trečiasis dėmuo nusako protonų Kulono stūmos potencinę energiją (su minuso ženklu). 4) Ketvirtasis dėmuo simetrijos dėmuo. Jis atspindi du veiksnius: a) dviejų skirtingų nukleonų vidutinė traukos jėga yra stipresnė negu dviejų vienodų; b) didėjant Z N ir esant pastoviam A, didėja nukleonų pilnutinė kinetinė energija Pirmojo veiksnio (a) įtakos apskaičiavimas: neutronų santykinė dalis yra f n = N / A, o protonų f p = Z / A. Dviejų nukleonų sąveikos (potencinė) energija yra u nn, u pp ir u np. Kadangi u nn = u pp = u, o u np u, tai pilnutinė nukleonų sąveikos energija yra u u ( N Z) Nuf ( n ufp) Z( ufn ufp) ( N 4 NZZ ) 3A A A 5) Penktasis dėmuo porų dėmuo atspindi vienodų nukleonų tendenciją jungtis į poras, kuriose abiejų nukleonų orbitinio judėjimo būsenos yra vienodos, o sukiniai yra priešingi. /3 1/3 1 ER AA Z( Z 1) A ( N Z) A C Savitosios ryšio energijos mažėjimas didėjant A didelių A srityje yra susijęs su didėjančiu santykiniu Kulono stūmos (trečiojo dėmens) vaidmeniu (didėjant A, didėja ir Z, o E R kvadratiškai priklauso nuo Z). Tai branduolinių reaktorių veikimo fizikinis pagrindas: šiuose reaktoriuose energija gaunama dalijantis nuklidų 35 U, 33 U arba 39 Pu branduoliams. Savitosios ryšio energijos mažėjimas mažėjant A mažų A srityje yra susijęs su didėjančia santykine dalimi nukleonų, kurie yra branduolio paviršiuje (t. y. didėja antrojo dėmens santykinis vaidmuo). Vadinasi, lengvųjų branduolių sintezę, kaip ir sunkiųjų branduolių dalijimąsi, galima panaudoti energijai gaminti. Tai yra ateities termobranduolinių reaktorių veikimo pagrindas. 45
46 Alfa skilimo aiškinimas remiantis kvantiniu tuneliniu efektu Kulono potencialo barjeras Geigerio ir Netolo dėsnis: lgt 1/ C D E Šį dėsnį paaiškina teorija, kurią 198 m. sukūrė rusų fizikas G. Gamovas. Alfa dalelės potencinė energija: Ze /(π x), kai x d, U( x) U, kai x d. dx dalelės ir antrinio branduolio sąveikos energijos priklausomybė nuo atstumo tarp jų dalelės išlėkimui iš branduolio egzistuoja potencialo barjeras, kurio aukštis Ze Umax U( d). π d Sunkiųjų branduolių d 1 14 m, Z 1, U max 3 MeV. Išlekiančių iš branduolio dalelių energija (48,7 MeV) yra mažesnė už barjero aukštį. Toks reiškinys, kai dalelė pereina pro potencialo barjerą, kurio aukštis didesnis už dalelės energiją, vadinamas tuneliniu reiškiniu. 46
47 Laisvos dalelės banginė funkcija ir tunelinis reiškinys Paprasčiausias potencialo barjeras yra vienmatis stačiakampis barjeras. I sritis: x < (į kairę nuo barjero, potencinė energija U = ), II sritis: x w (barjero vidus, potencinė energija U = U > E), III sritis: x > w (į dešinę nuo barjero, potencinė energija U = ). E x = x = w Dalelės banginė funkcija, kai egzistuoja potencialo barjeras, kurio aukštis yra didesnis už dalelės energiją Kadangi I ir III srityse dalelė yra laisva ir jos neveikia jokios jėgos, tai I ir III srityse dalelės banginė funkcija yra apibrėžto dažnio plokščioji banga. Atitinkamas bangos skaičius yra p me k1. h h II sritis ypatinga tuo, kad joje E < U. Klasikinėje mechanikoje tai nėra įmanoma. Kvantinėje mechanikoje tai yra įmanoma, nes, kai U kinta erdvėje, kinetinė energija neturi tiksliai apibrėžtos vertės (tik pilnutinė mechaninė energija E gali būti tiksliai apibrėžta). Potencialo barjero viduje, tolstant nuo barjero krašto, banginė funkcija mažėja eksponentiškai: ( x) ~ exp( kx ) ( x w), čia mu E ( ). k h Iš banginės funkcijos tolydumo sąlygos išplaukia, kad pakankamai siauro ir žemo potencinio barjero atveju banginė funkcija gali nespėti sumažėti iki nulio barjero viduje. Todėl egzistuoja tikimybė, jog dalelė prasiskverbs pro potencialo barjerą. Šis kvantinis reiškinys vadinamas tuneliniu reiškiniu arba tuneliavimu, o minėtoji tikimybė vadinama barjero skaidriu. Kai potencialo barjeras yra aukštas arba platus, t. y. kai galioja nelygybė kw 1, tada potencialo barjero skaidris yra apytiksliai lygus S exp( kw) exp m( U E) w1. h Bet kokio pavidalo barjero skaidris: N x S lim Sn exp m( U( x) E)d x; N n 1 h x 1 čia x 1 ir x yra lygties U(x) = E sprendiniai (potencialo barjero kraštų koordinatės dalelės energijos E lygyje). 47
48 Geigerio ir Netolo dėsnio išvedimas x 1 x Ze. π E ln S M( U( x) E)dx1. h x Jeigu dalelės greitis spindulio d branduolyje lygus v, tai dalelė atsiduria branduolio krašte vidutiniškai v/d kartų per laiko vienetą. Todėl skilimo konstanta lygi v S. d E = Mv /. Jeigu E = 1 MeV, tai v 1 7 m/s S [s ]. Kadangi T 1/ = ln /, lgt B.434ln S; 1/ Ze /(π x), kai x d, U( x) U, kai x d. Jeigu E << U (išskyrus integravimo rėžius, kuriuose U = E), tada, apytiksliai skaičiuojant, pointegralinis reiškinys proporcingas x 1/, o integralas proporcingas (x ) 1/, t. y. galima neatsižvelgti į dėmenį E po šaknies ženklu. Tada, įrašę U(x) išraišką (5.1.3) ir viršutiniojo rėžio išraišką (5.1.1) į (5.1.11) integralą, gauname, kad ln S proporcingas E 1/. 48
49 Neutrono pagavimo reakcijos skerspjūvio priklausomybė nuo neutrono greičio πr R n R n R b R b D (a) π( R D) R = R n + R b (b) Neutrono sukeltos branduolinės reakcijos skerspjūvio apskaičiavimas. (a) geometrinis artinys, (b) atsižvelgiant į neutrono koordinatės neapibrėžtumą Reakcijai vykti pakanka, kad vidutinis atstumas tarp dalelių paviršių taptų mažesnis už redukuotąjį bangos ilgį 1 D, k π čia yra neutrono de Broilio bangos ilgis h h. p m v Atitinkamas reakcijos skerspjūvis: π( R D ). 49
50 Energija Krintantysis neutronas Atspindėtasis neutronas E Perėjęs neutronas x U Branduolys Neutrono viršbarjerinis atspindys nuo branduolio sąlygoja papildomą daugiklį reakcijos skerspjūvio išraiškoje Neigiamo potencinės energijos šuolio skaidris : 4kk S ( k k) ; k me, k m ( EU ). D h h Potencialo šuolio skaidris S turi įeiti į reakcijos skerspjūvio išraišką kaip papildomas daugiklis: 4kk π( R D ). ( k k) Mažos energijos neutronams (kai E < 1 MeV) D R, E << U ir k << k'. Todėl 4k 4 S, k Dk 4 4 D 1 π D ~. D k k v 5
51 Rezonansai tarpinio branduolio reakcijose Tarpinio branduolio reakcijų skerspjūvio priklausomybėje nuo E dažnai būna maksimumai. Jie atsiranda tada, kai tarpinio branduolio sužadinimo energija tiksliai atitinka vieną iš jo sužadintųjų energijos lygmenų ( savųjų virpesių dažnių ). Šis reiškinys vadinamas rezonansu. Rezonanso srityje 1 ( E)~ ( E Er ) ( /) (tai yra vadinamoji Lorenco arba Breito ir Vignerio funkcija). Breito ir Vignerio rezonansinė kreivė Neutronų sąveikos su kadmio izotopu 113 Cd pilnutinis skerspjūvis. Matomas ryškus rezonansas ties neutrono energija,17 ev 51
52 Branduolių sintezė Energija Q, kuri išsiskiria susijungiant dviem branduoliams, kurių masės skaičiai A 1 ir A, į vieną branduolį, kurio masės skaičius A: Q ER ER1 ER Q A E AE AE AE AE ( AA) E R 1 R1 R R 1 R1 1 R A1( ER ER1) A( ER ER) Q ženklą lemia antrojo skirtumo ženklas. Todėl, kad Q būtų teigiamas, A 1 ir A vertės turi būti toje priklausomybės E R (A) srityje, kurioje E R didėja didėjant A. Tai atitinka lengvuosius branduolius E R / MeV Savitosios ryšio energijos priklausomybė () nuo branduolio masės skaičiaus A Lengviausia realizuoti mažiausio krūvio branduolių (vandenilio arba helio izotopų) sintezę. Reakcijų pavyzdžiai: deuterio-deuterio (D-D) reakcijos (žymuo d reiškia H, o t reiškia 3 H): d d 4 He arba d(d, ) 4 He (Q = 3,8 MeV) d d 3 He n arba d(d,n ) 3 He (Q = 3,3 MeV) d d t p arba d(d,p )t (Q = 4, MeV) deuterio-tričio (D-T) reakcija: d t 4 He n arba t(d,n ) 4 He (Q = 17,6 MeV) deuterio-helio reakcija: d 3 He 4 He p arba 3 He(d,p ) 4 He (Q = 18,35 MeV) A 5
53 Branduolių sintezės reakcijos produktų kinetinė energija Jeigu reakcijos metu atsiranda dvi nereliatyvistinės dalelės x ir Y (x lengvoji dalelė, o Y branduolys), tada xvx myvy m Q, mxvx myv Y. 1 Q 1 Q m,. 1 / 1 / xvx myv Y mx my my mx 1 1 m v x m v Y x Y m m Pvz., D-T reakcijoje 8 % visos išsiskyrusios energijos nusineša neutronas Branduolių sintezės reakcijos skerspjūvis Y x Didžiausias galimas reakcijos skerspjūvis: π( R D ) Kai reaguoja vandenilio izotopų branduoliai, kurių energija yra ~1 kev, tada R D, Todėl π πh h πd k p 4πm v Tikrasis sintezės reakcijos skerspjūvis yra mažesnis dėl reaguojančių branduolių Kulono stūmos, kurios energija lygi e Z1Z U() r 4π r Energija U(r) E R = R 1 + R R' r Kulono potencialo barjeras branduolių sintezei 53
54 Kulono potencialo barjero aukštis: e Z1Z Uc 4π R1 R Branduoliai susijungia tik po tuneliavimo pro šį barjerą. Todėl skerspjūvio išraiškoje atsiranda papildomas daugiklis barjero skaidris D: R h G 1 D, De, G m( U( r) E) dr 4πm v h čia G yra Gamovo faktorius. R' yra atstumas, kur krintančiojo branduolio energija tampa lygi Kulono stūmos energijai, t. y. lygties U(r) = E sprendinys: 1 Z1Ze R 4π E Įrašius šią R išraišką į G išraišką ir apskaičiavus integralą, gaunama m ZZe 1 G [arccos x x(1 x)], h E 4π čia x = R / R' = E / U c. Kadangi x << 1, tai reiškinys laužtiniuose skliaustuose yra apytiksliai lygus /. Kadangi m / E = / v, tai e πz1z e Z1Z G 4π hv 4 hv ; čia v yra reaguojančių branduolių reliatyvusis greitis. Galutinė reakcijos skerspjūvio išraiška: h 1 e Z1Z exp 4πm v hv T. y. 1 G 1 ~ e ; G ~ v v Todėl, didėjant greičiui v, skerspjūvis didėja. Taip yra todėl, kad mažėja potencialo barjero plotis R R. Reakcijos sparta mv Maksvelo skirstinys: p( v)~ v exp kt Kad realizuoti termobranduolinę reakciją, branduolių mišinį reikia įkaitinti iki temperatūros, kurioje kt yra 1 kev eilės. Tai atitinka 1 8 K eilės temperatūrą. Reakcijos sparta R tai sintezuojamų branduolių skaičius tūrio vienete per laiko vienetą. Jeigu reaguoja skirtingi branduoliai, kurių koncentracijos n 1 ir n, tada R = n 1 n v. Atsižvelgus į greičio v pasiskirstymą, Rnn 1 v, R v p( v) ( v) vdv 54
55 Maksvelo skirstinio tikimybės tankio p ir reliatyviojo greičio v bei reakcijos skerspjūvio sandaugos v priklausomybė nuo v 3 m /s vσ Vidurkio v vertės kelioms sintezės reakcijoms kt Valdomos termobranduolinės reakcijos sąlygos Termobranduolinės sintezės sąlygomis branduolinis kuras yra plazmos būsenos, t. y. elektriškai neutralus branduolių ir elektronų mišinys. Tarpinė stadija prieš realizuojant valdomą branduolių sintezę lygybės taškas (angl. break-even point). Tai yra tokia būsena, kai dėl branduolių sintezės per laiko vienetą išsiskiriantis energijos kiekis yra lygus galiai, kurią reikia išeikvoti tam, kad būtų palaikomi plazmos temperatūra bei slėgis. Plazmą kaitina tik stipriai sugeriamos dalelės, kurios lieka plazmoje (pvz., dalelės). Neutronai išeina iš reakcijos srities, nusinešdami dalį energijos. Todėl lygybės taško sąlygomis dar yra reikalingi išoriniai energijos šaltiniai. Kita stadija uždegimo taškas, t. y. tokia būsena, kai dalelių energijos pakanka tam, kad palaikyti reakcijos sąlygas. Tada išoriniai energijos šaltiniai tampa nereikalingi. kev 55
Microsoft Word - Liuminescencija_teorija
 2. BOLOGNŲ OBJEKTŲ LUMNESCENCJA. 2.1 Įvadas. Liuminescencijos reiškinys Daugelis fotofizikinių ir fotocheminių vyksmų yra šviesos sąveikos su bioobjektu pasekmės. Vienas iš pagrindinių šviesos emisijos
2. BOLOGNŲ OBJEKTŲ LUMNESCENCJA. 2.1 Įvadas. Liuminescencijos reiškinys Daugelis fotofizikinių ir fotocheminių vyksmų yra šviesos sąveikos su bioobjektu pasekmės. Vienas iš pagrindinių šviesos emisijos
LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS ŠVIESOS BANGINĖS SAVYBĖS. ATOMO SANDARA.
 LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS ŠVIESOS BANGINĖS SAVYBĖS. ATOMO SANDARA. LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS ŠVIESOS
LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS ŠVIESOS BANGINĖS SAVYBĖS. ATOMO SANDARA. LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS ŠVIESOS
Darbas Nr Aplinkos radiacinio fono matavimas dozimetrais
 VILNIAUS UNIVERSITETAS Fizikos fakultetas Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. 18 APLINKOS RADIACINIO FONO MATAVIMAS DOZIMETRAIS Parengė A. Poškus 2019-02-04 Turinys 1. UŽDUOTYS...
VILNIAUS UNIVERSITETAS Fizikos fakultetas Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. 18 APLINKOS RADIACINIO FONO MATAVIMAS DOZIMETRAIS Parengė A. Poškus 2019-02-04 Turinys 1. UŽDUOTYS...
LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 7. PAPRASČIAUSIOS DIFERENCIALINĖS LYGTYS ( ) Teorinę medžiagą parengė ir septintąją užduotį sudarė prof. d
 LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 7 PAPRASČIAUSIOS DIFERENIALINĖS LYGTYS (07 09) Teorinę medžiagą parengė ir septintąją užduotį sudarė prof dr Eugenijus Stankus Diferencialinės lygtys taikomos sprendžiant
LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 7 PAPRASČIAUSIOS DIFERENIALINĖS LYGTYS (07 09) Teorinę medžiagą parengė ir septintąją užduotį sudarė prof dr Eugenijus Stankus Diferencialinės lygtys taikomos sprendžiant
Microsoft Word - 8 Laboratorinis darbas.doc
 Laboratorinis darbas Nr. 8 MOP (metalo sido puslaidininkio) struktūrų tyrimas aukštadažniu -V charakteristikų metodu Darbo tikslas: 1. Nustatyti puslaidininkio laidumo tipą. 2. Nustatyti legiravimo priemaišų
Laboratorinis darbas Nr. 8 MOP (metalo sido puslaidininkio) struktūrų tyrimas aukštadažniu -V charakteristikų metodu Darbo tikslas: 1. Nustatyti puslaidininkio laidumo tipą. 2. Nustatyti legiravimo priemaišų
Darbas Nr Atmosferos užterštumo radijo nuklidais ir medžiagų tūrinio radioaktyviojo užterštumo tyrimas
 VILNIAUS UNIVERSITETAS Fizikos fakultetas Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. 17 ATMOSFEROS UŽTERŠTUMO RADIJO NUKLIDAIS IR MEDŽIAGŲ TŪRINIO RADIOAKTYVIOJO UŽTERŠTUMO TYRIMAS
VILNIAUS UNIVERSITETAS Fizikos fakultetas Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. 17 ATMOSFEROS UŽTERŠTUMO RADIJO NUKLIDAIS IR MEDŽIAGŲ TŪRINIO RADIOAKTYVIOJO UŽTERŠTUMO TYRIMAS
Microsoft PowerPoint - ikaitinti_kunai02.ppt
 Šviesos šaltiniai Nekoherentiniai šviesos šaltiniai. Šviesos šaltinių rūšys. Absoliučiai juodo kūno spinduliavimas. Kaitinimo lempos. Dujų išlydžio lempos. Šviestukų veikimo fizikiniai principai ir technologijos.
Šviesos šaltiniai Nekoherentiniai šviesos šaltiniai. Šviesos šaltinių rūšys. Absoliučiai juodo kūno spinduliavimas. Kaitinimo lempos. Dujų išlydžio lempos. Šviestukų veikimo fizikiniai principai ir technologijos.
DĖL APLINKOS IR SVEIKATOS MOKSLO KOMITETO ĮSTEIGIMO
 LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRAS ĮSAKYMAS DĖL LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRO 011 M. KOVO D. ĮSAKYMO NR. V-199 DĖL LIETUVOS HIGIENOS NORMOS HN 80:011 ELEKTROMAGNETINIS
LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRAS ĮSAKYMAS DĖL LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRO 011 M. KOVO D. ĮSAKYMO NR. V-199 DĖL LIETUVOS HIGIENOS NORMOS HN 80:011 ELEKTROMAGNETINIS
* # * # # 1 TIESĖS IR PLOKŠTUMOS 1 1 Tiesės ir plokštumos 1.1 Lygtys ir taškų aibės Sferos lygtis Tarkime, kad erdvėje apibrėžta Dekarto stačiak
 1 TIESĖS IR PLOKŠTUMOS 1 1 Tiesės ir plokštumos 1.1 Lygtys ir taškų aibės 1.1.1 Sferos lygtis Tarkime kad erdvėje apibrėžta Dekarto stačiakampė koordinačių sistema Sfera su centru taške ir spinduliu yra
1 TIESĖS IR PLOKŠTUMOS 1 1 Tiesės ir plokštumos 1.1 Lygtys ir taškų aibės 1.1.1 Sferos lygtis Tarkime kad erdvėje apibrėžta Dekarto stačiakampė koordinačių sistema Sfera su centru taške ir spinduliu yra
8. Daugiakanalė sklaidos teorija Stipraus ryšio tarp kanalu metodas Nagrinėsime sklaidos procesa x + A x + A, x + A x + A, nenaudodami perturbaciju te
 8. Daugiakanalė sklaidos teorija Stipraus ryšio tarp kanalu metodas Nagrinėsime sklaidos procesa x + A x + A, x + A x + A, nenaudodami perturbaciju teorijos. Tegul ξ bus taikinio A vidiniu kintamu ju rinkinys,
8. Daugiakanalė sklaidos teorija Stipraus ryšio tarp kanalu metodas Nagrinėsime sklaidos procesa x + A x + A, x + A x + A, nenaudodami perturbaciju teorijos. Tegul ξ bus taikinio A vidiniu kintamu ju rinkinys,
Microsoft Word ratas 12kl Spr
 66-iosios Lietuvos okinių fizikos olipiados rajono iesto turas (8 ) klasė Nedidelis kūnas be pradinio greičio nuslysta nuožulniąja plokštua, kurios papėdėje glotniai pasiekia horizontaliąją h plokštuą,
66-iosios Lietuvos okinių fizikos olipiados rajono iesto turas (8 ) klasė Nedidelis kūnas be pradinio greičio nuslysta nuožulniąja plokštua, kurios papėdėje glotniai pasiekia horizontaliąją h plokštuą,
13/6 t. LT Europos Sąjungos oficialusis leidinys L0181 L 39/40 EUROPOS BENDRIJŲ OFICIALUSIS LEIDINYS TARYBOS DIREKTYVA 1979 m. gruodž
 3 31980L0181 L 39/40 EUROPOS BENDRIJŲ OFICIALUSIS LEIDINYS 1980 2 15 TARYBOS DIREKTYVA 1979 m. gruodžio 20 d. dėl valstybių narių įstatymų, susijusių su matavimo vienetais, suderinimo ir Direktyvos 71/354/EEB
3 31980L0181 L 39/40 EUROPOS BENDRIJŲ OFICIALUSIS LEIDINYS 1980 2 15 TARYBOS DIREKTYVA 1979 m. gruodžio 20 d. dėl valstybių narių įstatymų, susijusių su matavimo vienetais, suderinimo ir Direktyvos 71/354/EEB
10 Pratybos Oleg Lukašonok 1
 10 Pratybos Oleg Lukašonok 1 2 Tikimybių pratybos 1 Lema Lema 1. Tegul {Ω, A, P} yra tikimybinė erdvė. Jeigu A n A, n N, tai i) P (lim sup A n ) = P ( k=1 n=k A n ) = lim P ( n k n=ka n ), nes n=ka n monotoniškai
10 Pratybos Oleg Lukašonok 1 2 Tikimybių pratybos 1 Lema Lema 1. Tegul {Ω, A, P} yra tikimybinė erdvė. Jeigu A n A, n N, tai i) P (lim sup A n ) = P ( k=1 n=k A n ) = lim P ( n k n=ka n ), nes n=ka n monotoniškai
Lietuvos energetikos instituto
 LIETUVOS ENERGETIKOS INSTITUTO ŠILUMINIŲ ĮRENGIMŲ TYRIMO IR BANDYMŲ LABORATORIJA AKREDITAVIMO SRITIS (Lanksti sritis) 1(11) puslapis 1. Membraniniai dujų skaitikliai, kurių didžiausias debitas Q max 16
LIETUVOS ENERGETIKOS INSTITUTO ŠILUMINIŲ ĮRENGIMŲ TYRIMO IR BANDYMŲ LABORATORIJA AKREDITAVIMO SRITIS (Lanksti sritis) 1(11) puslapis 1. Membraniniai dujų skaitikliai, kurių didžiausias debitas Q max 16
Elektronu igreitejimo stipriame elektriniame lauke itaka fotolaidžios terahercu antenos savybems
 Elektronu igreitejimo stipriame elektriniame lauke itaka fotolaidºios terahercu antenos savybems Gediminas lekas 2019 05 07 VGTU Matematinio Modeliavimo Katedros seminaras 1 / 42 Padeka Podoktorant uros
Elektronu igreitejimo stipriame elektriniame lauke itaka fotolaidºios terahercu antenos savybems Gediminas lekas 2019 05 07 VGTU Matematinio Modeliavimo Katedros seminaras 1 / 42 Padeka Podoktorant uros
PS_riba_tolydumas.dvi
 Funkcijos riba ir tolydumas Ribos apibrėžimas Nykstamosios funkcijos Funkcijos riba, kai x + Skaičių sekos riba Neaprėžtai didėjančios funkcijos Neapibrėžtumai Vienpusės ribos Funkcijos tolydumas Funkcijos
Funkcijos riba ir tolydumas Ribos apibrėžimas Nykstamosios funkcijos Funkcijos riba, kai x + Skaičių sekos riba Neaprėžtai didėjančios funkcijos Neapibrėžtumai Vienpusės ribos Funkcijos tolydumas Funkcijos
9 paskaita 9.1 Erdvės su skaliarine daugyba Šiame skyriuje nagrinėsime abstrakčias tiesines erdves, kurioms apibrėžta skaliarinė daugyba. Jos sudaro l
 9 paskaita 9.1 Erdvės su skaliarine daugyba Šiame skyriuje nagrinėsime abstrakčias tiesines erdves, kurioms apibrėžta skaliarinė daugyba. Jos sudaro labai svarbu normuotu ju erdviu šeimos pošeimį. Pilnosios
9 paskaita 9.1 Erdvės su skaliarine daugyba Šiame skyriuje nagrinėsime abstrakčias tiesines erdves, kurioms apibrėžta skaliarinė daugyba. Jos sudaro labai svarbu normuotu ju erdviu šeimos pošeimį. Pilnosios
Microsoft PowerPoint Dvi svarbios ribos [Read-Only]
![Microsoft PowerPoint Dvi svarbios ribos [Read-Only] Microsoft PowerPoint Dvi svarbios ribos [Read-Only]](/thumbs/88/116285598.jpg) Dvi svarbios ribos Nykstamųjų funkcijų palyginimas. Ekvivalenčios nykstamosios funkcijos. Funkcijos tolydumo taške apibrėžimas. Tolydžiųjų funkcijų atkarpoje savybės. Trūkiosios funkcijos. Trūko taškų
Dvi svarbios ribos Nykstamųjų funkcijų palyginimas. Ekvivalenčios nykstamosios funkcijos. Funkcijos tolydumo taške apibrėžimas. Tolydžiųjų funkcijų atkarpoje savybės. Trūkiosios funkcijos. Trūko taškų
(Microsoft Word - Pasiruo\360imas EE 10 KD-1)
 -as kontrolinis darbas (KD-) Kompleksiniai skaičiai. Algebrinė kompleksinio skaičiaus forma Pagrindinės sąvokos apibrėžimai. Veiksmai su kompleksinio skaičiais. 2. Kompleksinio skaičiaus geometrinis vaizdavimas.
-as kontrolinis darbas (KD-) Kompleksiniai skaičiai. Algebrinė kompleksinio skaičiaus forma Pagrindinės sąvokos apibrėžimai. Veiksmai su kompleksinio skaičiais. 2. Kompleksinio skaičiaus geometrinis vaizdavimas.
MatricosDetermTiesLS.dvi
 MATRICOS Matricos. Pagrindiniai apibrėžimai a a 2... a n a 2 a 22... a 2n............ a m a m2... a mn = a ij m n matrica skaičių lentelė m eilučių skaičius n stulpelių skaičius a ij matricos elementas
MATRICOS Matricos. Pagrindiniai apibrėžimai a a 2... a n a 2 a 22... a 2n............ a m a m2... a mn = a ij m n matrica skaičių lentelė m eilučių skaičius n stulpelių skaičius a ij matricos elementas
ŠIAULIŲ MUNICIPALINĖ APLINKOS TYRIMŲ LABORATORIJA Gegužių g. 94, Šiauliai. Įmonės kodas Tel. : +370 (41) ; el.p.:
 ŠIAULIŲ MUNICIPALINĖ APLINKOS TYRIMŲ LABORATORIJA Gegužių g. 94, 78365 Šiauliai. Įmonės kodas 145412194. Tel. : +370 (41) 51 41 44; el.p.: matl@splius.lt; www.matl.lt. ŠIAULIŲ MUNICIPALINIS PAVIRŠINIŲ
ŠIAULIŲ MUNICIPALINĖ APLINKOS TYRIMŲ LABORATORIJA Gegužių g. 94, 78365 Šiauliai. Įmonės kodas 145412194. Tel. : +370 (41) 51 41 44; el.p.: matl@splius.lt; www.matl.lt. ŠIAULIŲ MUNICIPALINIS PAVIRŠINIŲ
Atranka į 2019 m. Pasaulinę ir Vidurio Europos matematikos olimpiadas Sprendimai Artūras Dubickas ir Aivaras Novikas 1. Mykolas sugalvojo natūraliųjų
 Atranka į 019 m. Pasaulinę ir Vidurio Europos matematikos olimpiadas Sprendimai Artūras Dubickas ir Aivaras Novikas 1. Mykolas sugalvojo natūraliųjų skaičių seką a 1, a, a 3,..., o tada apibrėžė naują
Atranka į 019 m. Pasaulinę ir Vidurio Europos matematikos olimpiadas Sprendimai Artūras Dubickas ir Aivaras Novikas 1. Mykolas sugalvojo natūraliųjų skaičių seką a 1, a, a 3,..., o tada apibrėžė naują
Microsoft Word - Ch-vert-1-09.doc
 PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 009 m. birželio 6 d. įsakymu (..)-V-98 009 m. EMIJS VALSTYBINI BRANDS EGZAMIN UÞDUTIES VERTINIM INSTRUKIJA Kiekvienas I dalies klausimas vertinamas
PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 009 m. birželio 6 d. įsakymu (..)-V-98 009 m. EMIJS VALSTYBINI BRANDS EGZAMIN UÞDUTIES VERTINIM INSTRUKIJA Kiekvienas I dalies klausimas vertinamas
G E O M E T R I J A Gediminas STEPANAUSKAS Turinys 1 TIES ES IR PLOK TUMOS Plok²tumos ir tieses plok²tumoje normalines lygtys
 G E O M E T R I J A Gediminas STEPANAUSKAS 016 09 1 Turinys 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir tieses plok²tumoje normalines lygtys 111 Vektorine forma 11 Koordinatine forma 3 1 Bendroji plok²tumos
G E O M E T R I J A Gediminas STEPANAUSKAS 016 09 1 Turinys 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir tieses plok²tumoje normalines lygtys 111 Vektorine forma 11 Koordinatine forma 3 1 Bendroji plok²tumos
INW orpūtės ir oro siurbliai su šoniniu kanalu _ 1.1_Vienos pakopos 1.2_Dviejų pakopų 1.3_Aukšto slėgio Air and Vacuum Components
 INW orpūtės ir oro siurbliai su šoniniu kanalu _ 1.1_Vienos pakopos 1.2_Dviejų pakopų 1._Aukšto slėgio Air and Vacuum Components 1 INW orpūtės ir oro siurbliai su šoniniu kanalu _ Orpūtės / oro siurbliai
INW orpūtės ir oro siurbliai su šoniniu kanalu _ 1.1_Vienos pakopos 1.2_Dviejų pakopų 1._Aukšto slėgio Air and Vacuum Components 1 INW orpūtės ir oro siurbliai su šoniniu kanalu _ Orpūtės / oro siurbliai
Lietuvos mokinių matematikos olimpiada Rajono (miesto) etapo užduočių klasei sprendimai 2015 m. 1 uždavinys. Aistė užrašė skaičių seką: 1 (2 3)
 Lietuvos mokinių matematikos olimpiada Rajono (miesto) etapo užduočių 11-12 klasei sprendimai 2015 m. 1 uždavinys. Aistė užrašė skaičių seką: 1 (2 3) 4, 4 (5 6) 7, 7 (8 9) 10,..., 2014 (2015 2016) 2017.
Lietuvos mokinių matematikos olimpiada Rajono (miesto) etapo užduočių 11-12 klasei sprendimai 2015 m. 1 uždavinys. Aistė užrašė skaičių seką: 1 (2 3) 4, 4 (5 6) 7, 7 (8 9) 10,..., 2014 (2015 2016) 2017.
PowerPoint Presentation
 Algoritmai ir duomenų struktūros (ADS) 13 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2018-05-14 Šaltinis Paskaita parengta pagal William Pugh Skip Lists: A Probabilistic Alternative to
Algoritmai ir duomenų struktūros (ADS) 13 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2018-05-14 Šaltinis Paskaita parengta pagal William Pugh Skip Lists: A Probabilistic Alternative to
lec10.dvi
 paskaita. Euklido erdv_es. pibr_ezimas. Vektorin_e erdv_e E virs realiuju skaiciu kuno vadinama Euklido erdve, jeigu joje apibr_ezta skaliarin_e sandauga, t.y. tokia funkcija, kuri vektoriu porai u; v
paskaita. Euklido erdv_es. pibr_ezimas. Vektorin_e erdv_e E virs realiuju skaiciu kuno vadinama Euklido erdve, jeigu joje apibr_ezta skaliarin_e sandauga, t.y. tokia funkcija, kuri vektoriu porai u; v
Zona_2009
 2009 m. oro kokyb s tyrimų zonoje apžvalga Oro kokyb s vertinimui ir valdymui Lietuvos teritorijoje išskirtos Vilniaus ir Kauno aglomeracijos bei zona (likusi Lietuvos teritorija be Vilniaus ir Kauno miestų).
2009 m. oro kokyb s tyrimų zonoje apžvalga Oro kokyb s vertinimui ir valdymui Lietuvos teritorijoje išskirtos Vilniaus ir Kauno aglomeracijos bei zona (likusi Lietuvos teritorija be Vilniaus ir Kauno miestų).
TAIKOMOJI MATEMATIKA IR KIEKYBINIAI METODAI. Rašto darbas serija 3081 variantas Nustatykite funkcijos f(x) = x+2 x 6 cos ( 3x) apibrėžimo sritį.
 00 Nustatykite funkcijos f() = +2 6 cos ( 3) apibrėžimo sritį (, 0) (0, 2) (2, + ) 2 (, 2) ( 2, + ) 3 (, 2] 4 [ 2, + ) 5 [2, ) 6 (, 2] 7 (, + ) 8 [ 2, 0) (0, + ) 0 (, 2) (2, + ) { a + b, kai 7, Raskite
00 Nustatykite funkcijos f() = +2 6 cos ( 3) apibrėžimo sritį (, 0) (0, 2) (2, + ) 2 (, 2) ( 2, + ) 3 (, 2] 4 [ 2, + ) 5 [2, ) 6 (, 2] 7 (, + ) 8 [ 2, 0) (0, + ) 0 (, 2) (2, + ) { a + b, kai 7, Raskite
Techninis aprašymas RLV-KDV H tipo vožtuvas radiatoriams su integruotais termostatiniais vožtuvais užblokuojamas, su išleidimo galimybe ir integruotu
 H tipo vožtuvas radiatoriams su integruotais termostatiniais vožtuvais užblokuojamas, su išleidimo galimybe ir integruotu Taikymas Vožtuve yra integruotas slėgio perkryčio reguliatorius, užtikrinantis
H tipo vožtuvas radiatoriams su integruotais termostatiniais vožtuvais užblokuojamas, su išleidimo galimybe ir integruotu Taikymas Vožtuve yra integruotas slėgio perkryčio reguliatorius, užtikrinantis
Rekomendacijos vietinės reikšmės kelių su žvyro danga taisymui
 Rekomendacijos vietinės reikšmės kelių su žvyro danga taisymui LAKD TNT skyriaus vedėjas Evaldas Petrikas Reglamentavimas Automobilių kelių standartizuotų dangų konstrukcijų projektavimo taisyklės KPT
Rekomendacijos vietinės reikšmės kelių su žvyro danga taisymui LAKD TNT skyriaus vedėjas Evaldas Petrikas Reglamentavimas Automobilių kelių standartizuotų dangų konstrukcijų projektavimo taisyklės KPT
KROSNININKO SERTIFIKAVIMO schema
 Development of VET Training on Energy Efficient Stoves and Fireplaces ENEFFIS No. 2016-1-LT01-KA202-023161 KROSNININKO SERTIFIKAVIMO schema Parengė: VšĮ Vilniaus statybininkų rengimo centras Asociacija
Development of VET Training on Energy Efficient Stoves and Fireplaces ENEFFIS No. 2016-1-LT01-KA202-023161 KROSNININKO SERTIFIKAVIMO schema Parengė: VšĮ Vilniaus statybininkų rengimo centras Asociacija
MATEMATIKOS BRANDOS EGZAMINO PROGRAMOS MINIMALIUS REIKALAVIMUS ILIUSTRUOJANTYS PAVYZDŽIAI Egzamino programos minimalūs reikalavimai 1.3. Paprastais at
 MTEMTIKS BRNDS EGZMIN PRGRMS MINIMLIUS REIKLVIMUS ILIUSTRUJNTYS PVYZDŽII Egzamino programos minimalūs reikalavimai.. Paprastais atvejais patikrinti, ar duotoji seka ra aritmetinė/geometrinė progresija.
MTEMTIKS BRNDS EGZMIN PRGRMS MINIMLIUS REIKLVIMUS ILIUSTRUJNTYS PVYZDŽII Egzamino programos minimalūs reikalavimai.. Paprastais atvejais patikrinti, ar duotoji seka ra aritmetinė/geometrinė progresija.
Teorinių kontrolinių sąlygos ir sprendimai Vytautas Kazakevičius 2016 m. gruodžio 20 d. Teiginiai ( ). 1. (0.05 t.) Užrašykite formule tokį t
 Teorinių kontrolinių sąlygos sprendimai Vytautas Kazakevičius 206 m. gruodžio 20 d. Teiginiai (206-09-4).. (0.05 t.) Užrašykite formule tokį teiginį: jei iš dviejų teigiamų skaičių vienas yra mažesnis
Teorinių kontrolinių sąlygos sprendimai Vytautas Kazakevičius 206 m. gruodžio 20 d. Teiginiai (206-09-4).. (0.05 t.) Užrašykite formule tokį teiginį: jei iš dviejų teigiamų skaičių vienas yra mažesnis
VIEŠO NAUDOJIMO Aplinkos oro teršalų koncentracijos tyrimų, atliktų 2017 m. rugpjūčio d. Šiltnamių g. 23 Vilniaus mieste, naudojant mobiliąją la
 Aplinkos oro teršalų koncentracijos tyrimų, atliktų 2017 m. rugpjūčio 11 25 d. Šiltnamių g. 23 Vilniaus mieste, naudojant mobiliąją laboratoriją, rezultatų apžvalga Vilnius, 2017 m. Turinys Įžanga... 3
Aplinkos oro teršalų koncentracijos tyrimų, atliktų 2017 m. rugpjūčio 11 25 d. Šiltnamių g. 23 Vilniaus mieste, naudojant mobiliąją laboratoriją, rezultatų apžvalga Vilnius, 2017 m. Turinys Įžanga... 3
Radiacija ir jospoveikis
 Jonizuojančioji spinduliuotė Parengė: Radviliškio Lizdeikos gimnazijos 4C klasės mokinės Lina Peseckytė ir Armanda Kavaliauskaitė Konsultavo mokytoja J.Caporkienė Radiacija buvo visuomet: ji buvo prieš
Jonizuojančioji spinduliuotė Parengė: Radviliškio Lizdeikos gimnazijos 4C klasės mokinės Lina Peseckytė ir Armanda Kavaliauskaitė Konsultavo mokytoja J.Caporkienė Radiacija buvo visuomet: ji buvo prieš
VI. TOLYDŽIU IR DIFERENCIJUOJAMU FUNKCIJU TEOREMOS 6.1 Teoremos apie tolydžiu funkciju tarpines reikšmes Skaitytojui priminsime, kad nagrinėdami reali
 VI TOLYDŽIU IR DIFERENCIJUOJAMU FUNKCIJU TEOREMOS 61 Teoremos apie tolydžiu tarpines reikšmes Skaitytojui priminsime, kad nagrinėdami realiu ju skaičiu savybes atkreipėme dėmesi i tokia šios aibės elementu
VI TOLYDŽIU IR DIFERENCIJUOJAMU FUNKCIJU TEOREMOS 61 Teoremos apie tolydžiu tarpines reikšmes Skaitytojui priminsime, kad nagrinėdami realiu ju skaičiu savybes atkreipėme dėmesi i tokia šios aibės elementu
Isvestiniu_taikymai.dvi
 IŠVESTINIŲ TAIKYMAI Pagrindinės analizės teoremos Monotoninės funkcijos išvestinė Funkcijos ekstremumai Funkcijos didžiausia ir mažiausia reikšmės intervale Kreivės iškilumas Funkcijos grafiko asimptotės
IŠVESTINIŲ TAIKYMAI Pagrindinės analizės teoremos Monotoninės funkcijos išvestinė Funkcijos ekstremumai Funkcijos didžiausia ir mažiausia reikšmės intervale Kreivės iškilumas Funkcijos grafiko asimptotės
17 - Techniniai reikalavimai breziniuose.doc
 17. 17.1. Techniniai reikalavimai daro rėžiniuose Laisvų matmenų (matmenų, kurių nuokrypiai nenurodyti) ir nenurodyti padėties ei formos nuokrypiai turi atitikti nuokrypių klases, nusakomas ISO 2768 ir
17. 17.1. Techniniai reikalavimai daro rėžiniuose Laisvų matmenų (matmenų, kurių nuokrypiai nenurodyti) ir nenurodyti padėties ei formos nuokrypiai turi atitikti nuokrypių klases, nusakomas ISO 2768 ir
CL2013O0023LT _cp 1..1
 02013O0023 LT 01.09.2018 001.001 1 Šis tekstas yra skirtas tik informacijai ir teisinės galios neturi. Europos Sąjungos institucijos nėra teisiškai atsakingos už jo turinį. Autentiškos atitinkamų teisės
02013O0023 LT 01.09.2018 001.001 1 Šis tekstas yra skirtas tik informacijai ir teisinės galios neturi. Europos Sąjungos institucijos nėra teisiškai atsakingos už jo turinį. Autentiškos atitinkamų teisės
Individualus projektas Programa TE-PM, TE-PS, TE-SL, TEstream 4, TEstream 6, TEstream 8, TEstreamOBD 4, TEstreamOBD 6, TEstreamOBD 8 sistemų naudotoja
 Individualus projektas Programa TE-PM, TE-PS, TE-SL, TEstream 4, TEstream 6, TEstream 8, TEstreamOBD 4, TEstreamOBD 6, TEstreamOBD 8 sistemų naudotojams Alternatyvus valdymo pultas telefone ViPGaS programos
Individualus projektas Programa TE-PM, TE-PS, TE-SL, TEstream 4, TEstream 6, TEstream 8, TEstreamOBD 4, TEstreamOBD 6, TEstreamOBD 8 sistemų naudotojams Alternatyvus valdymo pultas telefone ViPGaS programos
VISŲ TIPŲ IR GAMINTOJŲ MEMBRANINIAI DUJŲ SKAITIKLIAI 1. Skaitiklių savybės. Visų tipų ir gamintojų membraniniai dujų skaitikliai indikuoja vieną rodme
 VISŲ TIPŲ IR GAMINTOJŲ MEMBRANINIAI DUJŲ SKAITIKLIAI 1. Skaitiklių savybės. Visų tipų ir gamintojų membraniniai dujų skaitikliai indikuoja vieną rodmenį. Jeigu įrengtas tik membraninis dujų skaitiklis,
VISŲ TIPŲ IR GAMINTOJŲ MEMBRANINIAI DUJŲ SKAITIKLIAI 1. Skaitiklių savybės. Visų tipų ir gamintojų membraniniai dujų skaitikliai indikuoja vieną rodmenį. Jeigu įrengtas tik membraninis dujų skaitiklis,
STANDARTŲ RENGĖJŲ MOKYMAI
 PATVIRTINTA VšĮ Vilniaus Jeruzalės darbo rinkos mokymo centro direktoriaus 2015 m. rugpjūčio 31 d. įsakymu Nr. V-110 TARPTAUTINIO SUVIRINTOJO NEFORMALAUS MOKYMO PROGRAMA Programos kodas: 1508311101 Įgyjama
PATVIRTINTA VšĮ Vilniaus Jeruzalės darbo rinkos mokymo centro direktoriaus 2015 m. rugpjūčio 31 d. įsakymu Nr. V-110 TARPTAUTINIO SUVIRINTOJO NEFORMALAUS MOKYMO PROGRAMA Programos kodas: 1508311101 Įgyjama
Rockwool LIETUVA Grindų šiltinimas Tarpauštinių perdangų ir grindų ant grunto šilumos ir garso izoliacija
 Rockwool LIETUVA Grindų šiltinimas Tarpauštinių perdangų ir grindų ant grunto šilumos ir garso izoliacija Garso izoliavimas SMŪGIO GARSO IZOLIAVIMAS Smūgio garso izoliavimo rodiklis nusako tarpaukštinės
Rockwool LIETUVA Grindų šiltinimas Tarpauštinių perdangų ir grindų ant grunto šilumos ir garso izoliacija Garso izoliavimas SMŪGIO GARSO IZOLIAVIMAS Smūgio garso izoliavimo rodiklis nusako tarpaukštinės
Lietuvos mobiliojo ryšio operatorių 30Mbit/s zonų skaičiavimo metodika
 MOBILIOJO RYŠIO OPERATORIŲ 30 MB/S APRĖPTIES SKAIČIAVIMAI RRT atliktos analizės rezultatų viešas aptarimas, Susisiekimo ministerija 2015 10 19 Lietuvos respublikos ryšių reguliavimo tarnyba Direktoriaus
MOBILIOJO RYŠIO OPERATORIŲ 30 MB/S APRĖPTIES SKAIČIAVIMAI RRT atliktos analizės rezultatų viešas aptarimas, Susisiekimo ministerija 2015 10 19 Lietuvos respublikos ryšių reguliavimo tarnyba Direktoriaus
MODENA MODENA midi MODENA mini Techninės charakteristikos ir instrukcijos 2018
 MODENA MODENA midi MODENA mini Techninės charakteristikos ir instrukcijos 08 Turinys MODENA Sistemos MODENA, MODENA HIDE charakteristikos Sistemos MODENA, MODENA HIDE sudedamosios dalys MODENA HIDE sistemos
MODENA MODENA midi MODENA mini Techninės charakteristikos ir instrukcijos 08 Turinys MODENA Sistemos MODENA, MODENA HIDE charakteristikos Sistemos MODENA, MODENA HIDE sudedamosios dalys MODENA HIDE sistemos
CL2007R1418LT bi_cp 1..1
 2007R1418 LT 23.07.2011 004.001 1 Šis dokumentas yra skirtas tik informacijai, ir institucijos nėra teisiškai atsakingos už jo turinį B KOMISIJOS REGLAMENTAS (EB) Nr. 1418/2007 2007 m. lapkričio 29 d.
2007R1418 LT 23.07.2011 004.001 1 Šis dokumentas yra skirtas tik informacijai, ir institucijos nėra teisiškai atsakingos už jo turinį B KOMISIJOS REGLAMENTAS (EB) Nr. 1418/2007 2007 m. lapkričio 29 d.
PowerPoint Presentation
 Sisteminės kontrolės priemonės moderniam šilumos tiekimui Vytautas Deksnys KTU multisensorinių sistemų laboratorija Tel. 8698 48828, 0037037 300541 Vytautas.Deksnys@ktu.lt Paskirtis Priemonės yra skirtos
Sisteminės kontrolės priemonės moderniam šilumos tiekimui Vytautas Deksnys KTU multisensorinių sistemų laboratorija Tel. 8698 48828, 0037037 300541 Vytautas.Deksnys@ktu.lt Paskirtis Priemonės yra skirtos
Techninis aprašymas Tolygaus valdymo pavara AME 435 Aprašymas Vožtuvo srauto reguliavimo funkciją. Srautą galima įvairiai reguliuoti nuo tiesinio iki
 Techninis aprašymas Tolygaus valdymo pavara AME 435 Aprašymas Vožtuvo srauto reguliavimo funkciją. Srautą galima įvairiai reguliuoti nuo tiesinio iki logaritminio arba atvirkščiai. Nuo svyravimų sauganti
Techninis aprašymas Tolygaus valdymo pavara AME 435 Aprašymas Vožtuvo srauto reguliavimo funkciją. Srautą galima įvairiai reguliuoti nuo tiesinio iki logaritminio arba atvirkščiai. Nuo svyravimų sauganti
Šiame sąsiuvinyje Jūs rasite keleto dalykų užduotis bei mokinio anketą
 Pagrindinės formulės Mechanika v v0 v = s/ t, a =, F = ma, F = mg, F Vg n = ρ sk, = Fs, N =, η = 100 %. t t v Šiluma m ρ =, Q = cm t, Q = λm, Q = Lm, Q = qm, η = 100 %. V Q Elektrodinamika q U l I =, I
Pagrindinės formulės Mechanika v v0 v = s/ t, a =, F = ma, F = mg, F Vg n = ρ sk, = Fs, N =, η = 100 %. t t v Šiluma m ρ =, Q = cm t, Q = λm, Q = Lm, Q = qm, η = 100 %. V Q Elektrodinamika q U l I =, I
VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS KVANTINĖS ELEKTRONIKOS KATEDRA MOKOMOJI LAZERIŲ LABORATORIJA Laboratorinis darbas Nr. KE 2 Laisvos veikos ki
 VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS KVANTINĖS ELEKTRONIKOS KATEDRA MOKOMOJI LAZERIŲ LABORATORIJA Laboratorinis darbas Nr. KE 2 Laisvos veikos kietakūnio IAG:Nd lazerio tyrimas Metodiniai nurodymai
VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS KVANTINĖS ELEKTRONIKOS KATEDRA MOKOMOJI LAZERIŲ LABORATORIJA Laboratorinis darbas Nr. KE 2 Laisvos veikos kietakūnio IAG:Nd lazerio tyrimas Metodiniai nurodymai
VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS BENDROSIOS FIZIKOS IR SPEKTROSKOPIJOS KATEDRA Rasa Platakytė ACETILACETONO DARINIŲ FOTODINAMINIŲ PROCESŲ IR
 VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS BENDROSIOS FIZIKOS IR SPEKTROSKOPIJOS KATEDRA Rasa Platakytė ACETILACETONO DARINIŲ FOTODINAMINIŲ PROCESŲ IR MOLEKULINIŲ KOMPLEKSŲ SU VANDENIU TYRIMAS Magistratūros
VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS BENDROSIOS FIZIKOS IR SPEKTROSKOPIJOS KATEDRA Rasa Platakytė ACETILACETONO DARINIŲ FOTODINAMINIŲ PROCESŲ IR MOLEKULINIŲ KOMPLEKSŲ SU VANDENIU TYRIMAS Magistratūros
Priedai_2016.indd
 1 testo užduočių vertinimo kriterijai Užd. Nr. Sprendimas ar atsakymas Taškai Vertinimas 1 Pasirinktas variantas D 1 Už teisingą atsakymą. 2 a) 939 1 Už teisingą atsakymą. 2 b) 1538 1 Už teisingą atsakymą.
1 testo užduočių vertinimo kriterijai Užd. Nr. Sprendimas ar atsakymas Taškai Vertinimas 1 Pasirinktas variantas D 1 Už teisingą atsakymą. 2 a) 939 1 Už teisingą atsakymą. 2 b) 1538 1 Už teisingą atsakymą.
Microsoft Word - KRS_2012_metine_Babenai
 UAB Grota Gamtos tyrimų centras Geologijos ir geografijos institutas Hidrogeologijos sektorius Babėnų buitinių atliekų sąvartyno teritorijos aplinkos monitoringas Ataskaita apie 2012 metų stebėjimo rezultatus
UAB Grota Gamtos tyrimų centras Geologijos ir geografijos institutas Hidrogeologijos sektorius Babėnų buitinių atliekų sąvartyno teritorijos aplinkos monitoringas Ataskaita apie 2012 metų stebėjimo rezultatus
Microsoft PowerPoint Ekstremumai_naujas
 Kelių kintamųjų funkcijos lokalūs ekstremumai. Ekstremumų egzistavimo būtina ir pakankama sąlygos. Sąlyginiai ekstremumai. Lagranžo daugikliai. Didžiausioji ir mažiausioji funkcijos reikšmės uždaroje srityje.
Kelių kintamųjų funkcijos lokalūs ekstremumai. Ekstremumų egzistavimo būtina ir pakankama sąlygos. Sąlyginiai ekstremumai. Lagranžo daugikliai. Didžiausioji ir mažiausioji funkcijos reikšmės uždaroje srityje.
Alytaus regiono uždaryto Pagirmuonių sąvartyno aplinkos monitoringo 2017 m. ataskaita Ūkio subjektų aplinkos monitoringo nuostatų 4 priedas ALYTAUS RE
 Ūkio subjektų aplinkos monitoringo nuostatų 4 priedas ALYTAUS REGIONO UŽDARYTO PAGIRMUONIŲ SĄVARTYNO APLINKOS MONITORINGO 2017 M. ATASKAITA I BENDROJI DALIS 1. Informacija apie ūkio subjektą: 1.1. teisinis
Ūkio subjektų aplinkos monitoringo nuostatų 4 priedas ALYTAUS REGIONO UŽDARYTO PAGIRMUONIŲ SĄVARTYNO APLINKOS MONITORINGO 2017 M. ATASKAITA I BENDROJI DALIS 1. Informacija apie ūkio subjektą: 1.1. teisinis
TECHNINIAI DUOMENYS Pramoniniai vartai
 TECHNINIAI DUOMENYS Pramoniniai vartai TURINYS 4 BĖGIAI 5...STD 6...LHR-FM 7...LHR-RM 8...STD-RM 9...HL-TM 10...VL-TM 11...HL-MM1 su konsole žemiau montuojamoms spyruoklėms 12...HL-MM2 su konsole žemiau
TECHNINIAI DUOMENYS Pramoniniai vartai TURINYS 4 BĖGIAI 5...STD 6...LHR-FM 7...LHR-RM 8...STD-RM 9...HL-TM 10...VL-TM 11...HL-MM1 su konsole žemiau montuojamoms spyruoklėms 12...HL-MM2 su konsole žemiau
TIESINĖ ALGEBRA Matricos ir determinantai Matricos. Transponuota matrica. Nulinė ir vienetinė matrica. Kvadratinė matrica. Antrosios ir trečiosios eil
 TIESINĖ ALGEBRA Matricos ir determinantai Matricos. Transponuota matrica. Nulinė ir vienetinė matrica. Kvadratinė matrica. Antrosios ir trečiosios eilės determinantai. Minorai ir adjunktai. Determinantų
TIESINĖ ALGEBRA Matricos ir determinantai Matricos. Transponuota matrica. Nulinė ir vienetinė matrica. Kvadratinė matrica. Antrosios ir trečiosios eilės determinantai. Minorai ir adjunktai. Determinantų
CarSense 303 M A G N E T I N Ė K I L P A N A U D O J I M O I N S T R U K C I J A
 CarSense 303 M A G N E T I N Ė K I L P A N A U D O J I M O I N S T R U K C I J A Turinys Produkto apžvalga 2 Specifikacija 3 Naudojimas 4 Nustatymai ir indikatoriai 7 Pajungimo kontaktai 8 Gedimų šalinimas
CarSense 303 M A G N E T I N Ė K I L P A N A U D O J I M O I N S T R U K C I J A Turinys Produkto apžvalga 2 Specifikacija 3 Naudojimas 4 Nustatymai ir indikatoriai 7 Pajungimo kontaktai 8 Gedimų šalinimas
CL2008L0100LT bi_cp 1..1
 2008L0100 LT 18.11.2008 000.001 1 Šis dokumentas yra skirtas tik informacijai, ir institucijos nėra teisiškai atsakingos už jo turinį B KOMISIJOS DIREKTYVA 2008/100/EB 2008 m. spalio 28 d. iš dalies keičianti
2008L0100 LT 18.11.2008 000.001 1 Šis dokumentas yra skirtas tik informacijai, ir institucijos nėra teisiškai atsakingos už jo turinį B KOMISIJOS DIREKTYVA 2008/100/EB 2008 m. spalio 28 d. iš dalies keičianti
55 C 35 C Logatherm WPL 31 A A ++ A + A B C D E F G A + A db kw kw 64 db /2013
 55 C 35 C A B C D E F G 28 30 27 28 29 31 db kw kw 64 db 2015 811/2013 A B C D E F G 2015 811/2013 Duomenys atitinka Reglamentų (ES) 811/2013 ir (ES) 813/2013 reikalavimus. Gaminio parametrai Simbolis
55 C 35 C A B C D E F G 28 30 27 28 29 31 db kw kw 64 db 2015 811/2013 A B C D E F G 2015 811/2013 Duomenys atitinka Reglamentų (ES) 811/2013 ir (ES) 813/2013 reikalavimus. Gaminio parametrai Simbolis
ŪKIO SUBJEKTŲ POŽEMINIO VANDENS MONITORINGAS PROGRAMŲ RENGIMO METODINĖS REKOMENDACIJOS VILNIUS 2000
 ŪKIO SUBJEKTŲ POŽEMINIO VANDENS MONITORINGAS PROGRAMŲ RENGIMO METODINĖS REKOMENDACIJOS VILNIUS 2000 UDK 504.43.064.36(083.13):061.5 ŪKIO SUBJEKTŲ POŽEMINIO VANDENS MONITORINGAS: programų rengimo metodinės
ŪKIO SUBJEKTŲ POŽEMINIO VANDENS MONITORINGAS PROGRAMŲ RENGIMO METODINĖS REKOMENDACIJOS VILNIUS 2000 UDK 504.43.064.36(083.13):061.5 ŪKIO SUBJEKTŲ POŽEMINIO VANDENS MONITORINGAS: programų rengimo metodinės
21. Ilgis, plotas, perimetras Įvadas Šiame modulyje pateikti įvairaus sudėtingumo uždaviniai apie ilgį, perimetrą ir plotą. Sprendžiant uždavinius rei
 Įvadas Šiame modulyje pateikti įvairaus sudėtingumo uždaviniai apie ilgį, perimetrą ir plotą. Sprendžiant uždavinius reikės pasitelkti kūrybinį mąstymą ir pasinaudoti jau turimomis žiniomis, įgytomis per
Įvadas Šiame modulyje pateikti įvairaus sudėtingumo uždaviniai apie ilgį, perimetrą ir plotą. Sprendžiant uždavinius reikės pasitelkti kūrybinį mąstymą ir pasinaudoti jau turimomis žiniomis, įgytomis per
5_3 paskaita
 EKONOMIKOS INŽINERIJA Parengė: doc. dr. Vilda Gižienė 4. PRODUKTO GAMYBOS TECHNOLOGIJA Temos: 4.7.Įmonės pelnas ir jo maksimizavimas 4.7.1. Konkuruojančios firmos pajamos. 4.7.2. Pelno maksimizavimas trumpuoju
EKONOMIKOS INŽINERIJA Parengė: doc. dr. Vilda Gižienė 4. PRODUKTO GAMYBOS TECHNOLOGIJA Temos: 4.7.Įmonės pelnas ir jo maksimizavimas 4.7.1. Konkuruojančios firmos pajamos. 4.7.2. Pelno maksimizavimas trumpuoju
Microsoft Word - BABENU SAVARTYNAS 2011_I pusm aplinkos monit.
 BABĖNŲ SĄVARTYNO APLINKOS MONITORINGO 2011 M. I PUSMEČIO ATASKAITA I. BENDROJI DALIS 1. Ūkio objekto teisinė forma, pavadinimas ir adresas: VšĮ Kauno regiono atliekų tvarkymo centras (adresas: Statybininkų
BABĖNŲ SĄVARTYNO APLINKOS MONITORINGO 2011 M. I PUSMEČIO ATASKAITA I. BENDROJI DALIS 1. Ūkio objekto teisinė forma, pavadinimas ir adresas: VšĮ Kauno regiono atliekų tvarkymo centras (adresas: Statybininkų
Algebra ir geometrija informatikams. Paskaitu¾ konspektas Rimantas Grigutis 7 paskaita Matricos. 7.1 Apibr eµzimas. Matrica A yra m eiluµciu¾ir n stul
 lgebra ir geometrija informatikams. Paskaitu¾ konspektas Rimantas Grigutis 7 paskaita Matricos. 7. pibr eµzimas. Matrica yra m eiluµciu¾ir n stulpeliu¾turinti staµciakamp e lentel e su joje i¾rašytais
lgebra ir geometrija informatikams. Paskaitu¾ konspektas Rimantas Grigutis 7 paskaita Matricos. 7. pibr eµzimas. Matrica yra m eiluµciu¾ir n stulpeliu¾turinti staµciakamp e lentel e su joje i¾rašytais
Microsoft Word - Termodinamika.doc
 MOLEKULINĖ FIZIKA IR ERMODINAMIKA Pagrindinė idealiųjų dujų būsenos lygtis Idealiųjų dujų dėsniai Šiluinė ašina Koks yra deguonies tankis, kai teperatūra lygi 3K, o slėgis,6 Pa? Kokia yra ³ deguonies asė
MOLEKULINĖ FIZIKA IR ERMODINAMIKA Pagrindinė idealiųjų dujų būsenos lygtis Idealiųjų dujų dėsniai Šiluinė ašina Koks yra deguonies tankis, kai teperatūra lygi 3K, o slėgis,6 Pa? Kokia yra ³ deguonies asė
BASEINO OCTO+ 460, 540, 640 IR 840 MODELIO, AIKŠTELĖS PARUOŠIMAS IR MEDINIO KARKASO SURINKIMAS + LENTJUOSTES MONTAVIMAS + PATIESALO MONTAVIMAS Atlikit
 BASEINO OCTO+ 460, 540, 640 IR 840 MODELIO, AIKŠTELĖS PARUOŠIMAS IR MEDINIO KARKASO SURINKIMAS + LENTJUOSTES MONTAVIMAS + PATIESALO MONTAVIMAS Atlikite aikštelės nuţymėjimą po baseinu, pašalinkite augalus,
BASEINO OCTO+ 460, 540, 640 IR 840 MODELIO, AIKŠTELĖS PARUOŠIMAS IR MEDINIO KARKASO SURINKIMAS + LENTJUOSTES MONTAVIMAS + PATIESALO MONTAVIMAS Atlikite aikštelės nuţymėjimą po baseinu, pašalinkite augalus,
Honda GL1800 GOLD WING TOUR Gold Wing Tour Pasirodžius naujausiai legendinio Honda Gold Wing motociklo versijai šis neprilygstamas turistinis motocikl
 Honda GL1800 GOLD WING TOUR Gold Wing Tour Pasirodžius naujausiai legendinio Honda Gold Wing motociklo versijai šis neprilygstamas turistinis motociklas tapo dar universalesnis. Galima sakyti, kad šis
Honda GL1800 GOLD WING TOUR Gold Wing Tour Pasirodžius naujausiai legendinio Honda Gold Wing motociklo versijai šis neprilygstamas turistinis motociklas tapo dar universalesnis. Galima sakyti, kad šis
TAIKOMOJI MATEMATIKA. 1-ojo testo pavyzdžiai serija **** variantas 001 x x + 12 lim = x 4 2x 8 1 2; 3 0; 2 1 2; 5 1; 6 2; 7 ; riba nee
 001 x 1 2 + x + 12 lim x 4 2x 1 2; 0; 2 1 2; 5 1; 6 2; ; 1 2 4 riba neegzistuoja; 14x 2 2 + 29 lim x 1x 2 + 4x + 9 1 1; 2 29 9 ; ; 4 0; 5 riba neegzistuoja; 6 1 14; 14 1; 14 x + 1 lim x 4 x 4 1 riba neegzistuoja;
001 x 1 2 + x + 12 lim x 4 2x 1 2; 0; 2 1 2; 5 1; 6 2; ; 1 2 4 riba neegzistuoja; 14x 2 2 + 29 lim x 1x 2 + 4x + 9 1 1; 2 29 9 ; ; 4 0; 5 riba neegzistuoja; 6 1 14; 14 1; 14 x + 1 lim x 4 x 4 1 riba neegzistuoja;
EGZAMINO PROGRAMOS MINIMALIUS REIKALAVIMUS ILIUSTRUOJANTYS PAVYZDŽIAI Egzamino programos minimalūs reikalavimai I. METODOLOGINIAI BIOLOGIJOS KLAUSIMAI
 EGZAMINO PROGRAMOS MINIMALIUS REIKALAVIMUS ILIUSTRUOJANTYS PAVYZDŽIAI Egzamino programos minimalūs reikalavimai I. METODOLOGINIAI BIOLOGIJOS KLAUSIMAI Minimalius reikalavimus iliustruojantys pavyzdžiai
EGZAMINO PROGRAMOS MINIMALIUS REIKALAVIMUS ILIUSTRUOJANTYS PAVYZDŽIAI Egzamino programos minimalūs reikalavimai I. METODOLOGINIAI BIOLOGIJOS KLAUSIMAI Minimalius reikalavimus iliustruojantys pavyzdžiai
Projektas
 Aplinkos apsaugos agentūrai ŪKIO SUBJEKTŲ APLINKOS MONITORINGO ATASKAITA 1. Informacija apie ūkio subjektą: 1.1. teisinis statusas: juridinis asmuo juridinio asmens struktūrinis padalinys (filialas, atstovybė)
Aplinkos apsaugos agentūrai ŪKIO SUBJEKTŲ APLINKOS MONITORINGO ATASKAITA 1. Informacija apie ūkio subjektą: 1.1. teisinis statusas: juridinis asmuo juridinio asmens struktūrinis padalinys (filialas, atstovybė)
UAB Utenos šilumos tinklai (šilumos tiekėjo ir (ar) karšto vandens tiekėjo pavadinimas) įm.k , PVM mokėtojo kodas LT , Pramonės g. 11
 UAB Utenos šilumos tinklai (šilumos tiekėjo ir (ar) karšto vandens tiekėjo pavadinimas) įm.k.183843314, PVM mokėtojo kodas LT838433113, Pramonės g. 11, LT-28216 Utena, tel. (8 389) 63 641, faks. (8 389)
UAB Utenos šilumos tinklai (šilumos tiekėjo ir (ar) karšto vandens tiekėjo pavadinimas) įm.k.183843314, PVM mokėtojo kodas LT838433113, Pramonės g. 11, LT-28216 Utena, tel. (8 389) 63 641, faks. (8 389)
ITC ISSN LIETUVOS ŠVIETIMAS SKAIČIAIS Lietuvos Respublikos švietimo ir mokslo ministerija Švietimo informacinių technologijų centras 2017 Ik
 ITC ISSN 2345-0991 LIETUVOS ŠVIETIMAS SKAIČIAIS Lietuvos Respublikos švietimo ir mokslo ministerija Švietimo informacinių technologijų centras 2017 Ikimokyklinis ir priešmokyklinis ugdymas 1 2 3 4 5 6
ITC ISSN 2345-0991 LIETUVOS ŠVIETIMAS SKAIČIAIS Lietuvos Respublikos švietimo ir mokslo ministerija Švietimo informacinių technologijų centras 2017 Ikimokyklinis ir priešmokyklinis ugdymas 1 2 3 4 5 6
Slide 1
 Duomenų struktūros ir algoritmai 12 paskaita 2019-05-08 Norint kažką sukonstruoti, reikia... turėti detalių. 13 paskaitos tikslas Susipažinti su python modulio add.py 1.1 versija. Sukurti skaitmeninį modelį
Duomenų struktūros ir algoritmai 12 paskaita 2019-05-08 Norint kažką sukonstruoti, reikia... turėti detalių. 13 paskaitos tikslas Susipažinti su python modulio add.py 1.1 versija. Sukurti skaitmeninį modelį
Microsoft Word - Awalift 80 Manual_LT.doc
 Nuotekų perpumpavimo įrenginys su nešmenų atskyrimu Awalift 80 Instaliavimo ir naudojimo instrukcija Puslapis 1 / 9 Bendra informacija Nuotekų perpumpavimo įrenginiai naudojami kai nuotekų vamzdis yra
Nuotekų perpumpavimo įrenginys su nešmenų atskyrimu Awalift 80 Instaliavimo ir naudojimo instrukcija Puslapis 1 / 9 Bendra informacija Nuotekų perpumpavimo įrenginiai naudojami kai nuotekų vamzdis yra
VIEŠO NAUDOJIMO CENTRINĖ TYRIMŲ LABORATORIJA Estijos aplinkos tyrimų centras Aplinkos oro kokybės vertinimo tyrimo Vilniaus Lazdynų seniūnijoje ataska
 CENTRINĖ TYRIMŲ LABORATORIJA Estijos aplinkos tyrimų centras Aplinkos oro kokybės vertinimo tyrimo Vilniaus Lazdynų seniūnijoje ataskaita 2018 m. spalio mėn. 2018 m. Talinas Projekto pavadinimas Aplinkos
CENTRINĖ TYRIMŲ LABORATORIJA Estijos aplinkos tyrimų centras Aplinkos oro kokybės vertinimo tyrimo Vilniaus Lazdynų seniūnijoje ataskaita 2018 m. spalio mėn. 2018 m. Talinas Projekto pavadinimas Aplinkos
GRAFŲ TEORIJA Pasirenkamasis kursas, Magistrantūra, 3 sem m. rudens semestras Parengė: Eugenijus Manstavičius Įvadas Pirmoji kurso dalis skirta
 GRAFŲ TEORIJA Pasirenkamasis kursas, Magistrantūra, 3 sem. 2018 m. rudens semestras Parengė: Eugenijus Manstavičius Įvadas Pirmoji kurso dalis skirta grafų algoritmams, tačiau apibrėžus gretimumo matricą
GRAFŲ TEORIJA Pasirenkamasis kursas, Magistrantūra, 3 sem. 2018 m. rudens semestras Parengė: Eugenijus Manstavičius Įvadas Pirmoji kurso dalis skirta grafų algoritmams, tačiau apibrėžus gretimumo matricą
Ataskaita_4F08-89
 FIZIKOS INSTITUTAS TVIRTINU: Instituto direktorius Prof. Vidmantas Remeikis 2009 m. sausio 30 d. RADIOLOGINIAI ORO TYRIMAI VILNIAUS MIESTE 2008 m. liepos 10 d. sutartis Nr. 4F08-89 (300S634) MOKSLO TYRIMŲ
FIZIKOS INSTITUTAS TVIRTINU: Instituto direktorius Prof. Vidmantas Remeikis 2009 m. sausio 30 d. RADIOLOGINIAI ORO TYRIMAI VILNIAUS MIESTE 2008 m. liepos 10 d. sutartis Nr. 4F08-89 (300S634) MOKSLO TYRIMŲ
1 Vaizdu vidurkinimas ir požymiu išskyrimas 1.1 Glodus vienmatis eksponentinis filtras Apibrėšime eksponentini tolydu kintamojo x filtra formule ( v σ
 Vaizdu vidurkinimas ir požymiu išskyrimas. Glodus vienmatis eksponentinis filtras Apibrėšime eksponentini tolydu kintamojo x filtra formule ( v (x) = + x ) e x, x (, ). () Čia yra filtro parametras. Kad
Vaizdu vidurkinimas ir požymiu išskyrimas. Glodus vienmatis eksponentinis filtras Apibrėšime eksponentini tolydu kintamojo x filtra formule ( v (x) = + x ) e x, x (, ). () Čia yra filtro parametras. Kad
Transformatorių pastočių (skirstomųjų punktų) 10 kV linijiniai narveliai
 Eil. Nr. PATVIRTINTA AB LESTO 2011 m. rugpjūčio 26 d. Elektros tinklo tarnybos direktoriaus-generalinio direktoriaus pavaduotojo nurodymu Nr. 365 TRANSFORMATORIŲ PASTOČIŲ (SKIRSTOMŲJŲ PUNKTŲ) 10 kv SEMI
Eil. Nr. PATVIRTINTA AB LESTO 2011 m. rugpjūčio 26 d. Elektros tinklo tarnybos direktoriaus-generalinio direktoriaus pavaduotojo nurodymu Nr. 365 TRANSFORMATORIŲ PASTOČIŲ (SKIRSTOMŲJŲ PUNKTŲ) 10 kv SEMI
PowerPoint Presentation
 Dalyko sando kodas (Course code) Dalyko aprašas MKFA714 Dalyko pavadinimas (Course title) Dėstytojo (-jų) pedagoginis vardas, vardas ir pavardė (Name and position of lecturer) Dalyko sando lygis (Level
Dalyko sando kodas (Course code) Dalyko aprašas MKFA714 Dalyko pavadinimas (Course title) Dėstytojo (-jų) pedagoginis vardas, vardas ir pavardė (Name and position of lecturer) Dalyko sando lygis (Level
RET2000 Elektronisis Skaitmeninis Termostatas su LCD
 MAKING MODERN LIVING POSSIBLE RET2000 B/M/MS Elektroninis skaitmeninis termostatas su LCD Danfoss Heating Montavimo vadovas Norėdami gauti išsamią spausdintą šių instrukcijų versiją, skambinkite Rinkodaros
MAKING MODERN LIVING POSSIBLE RET2000 B/M/MS Elektroninis skaitmeninis termostatas su LCD Danfoss Heating Montavimo vadovas Norėdami gauti išsamią spausdintą šių instrukcijų versiją, skambinkite Rinkodaros
Techninis aprašymas SONOMETER TM 1100 Ultragarsinis kompaktiškas energijos skaitiklis Aprašymas / taikymas MID tikrinimo sertifikato nr.: DE-10-MI004-
 SONOMETER TM 1100 Ultragarsinis kompaktiškas energijos skaitiklis Aprašymas / taikymas MID tikrinimo sertifikato nr.: DE-10-MI004-PTB003 SONOMETER 1100 tai ultragarsinis statinis kompaktiškas energijos
SONOMETER TM 1100 Ultragarsinis kompaktiškas energijos skaitiklis Aprašymas / taikymas MID tikrinimo sertifikato nr.: DE-10-MI004-PTB003 SONOMETER 1100 tai ultragarsinis statinis kompaktiškas energijos
AM_Ple_LegReport
 17.10.2018 A8-0288/178 Pakeitimas 178 Michel Dantin PPE frakcijos vardu Pranešimas Michel Dantin Žmonėms vartoti skirto vandens kokybė (COM(2017)0753 C8-0019/2018 2017/0332(COD)) A8-0288/2018 Pasiūlymas
17.10.2018 A8-0288/178 Pakeitimas 178 Michel Dantin PPE frakcijos vardu Pranešimas Michel Dantin Žmonėms vartoti skirto vandens kokybė (COM(2017)0753 C8-0019/2018 2017/0332(COD)) A8-0288/2018 Pasiūlymas
PowerPoint Presentation
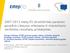 2007-2013 metų ES struktūrinės paramos poveikio Lietuvos miestams ir miesteliams vertinimo rezultatų pristatymas Neringa Viršilienė, ESTEP vertinimo grupės vadovė, vertinimo ekspertė Mindaugas Sereičikas,
2007-2013 metų ES struktūrinės paramos poveikio Lietuvos miestams ir miesteliams vertinimo rezultatų pristatymas Neringa Viršilienė, ESTEP vertinimo grupės vadovė, vertinimo ekspertė Mindaugas Sereičikas,
1 Priedas Prie Pardavimo sąlygų Nr. PRKS-4 PARDAVIMO OBJEKTO DUOMENYS Pardavimo objekto Nr. Pardavimo objekto pavadinimas Kiekis, vnt. Deta
 1 Priedas Prie 2019-05-28 sąlygų Nr. PRKS-4 PARDAVIMO OBJEKTO DUOMENYS objekto pavadinimas 1. Garo turbinos K-300-240-1 AS (aukšto slėgio) rotorius. 1 T-5*, brėžinio nr. А-1157694. 2. Garo turbinos K-300-240-1
1 Priedas Prie 2019-05-28 sąlygų Nr. PRKS-4 PARDAVIMO OBJEKTO DUOMENYS objekto pavadinimas 1. Garo turbinos K-300-240-1 AS (aukšto slėgio) rotorius. 1 T-5*, brėžinio nr. А-1157694. 2. Garo turbinos K-300-240-1
LIETUVOS RESPUBLIKOS ŪKIO MINISTRAS
 LIETUVOS RESPUBLIKOS ENERGETIKOS MINISTERIJA 2014 2020 M. EUROPOS SĄJUNGOS FONDŲ INVESTICIJŲ VEIKSMŲ PROGRAMOS PRIORITETO ĮGYVENDINIMO PRIEMONIŲ ĮGYVENDINIMO PLANAS I SKYRIUS 2014 2020 M. EUROPOS SĄJUNGOS
LIETUVOS RESPUBLIKOS ENERGETIKOS MINISTERIJA 2014 2020 M. EUROPOS SĄJUNGOS FONDŲ INVESTICIJŲ VEIKSMŲ PROGRAMOS PRIORITETO ĮGYVENDINIMO PRIEMONIŲ ĮGYVENDINIMO PLANAS I SKYRIUS 2014 2020 M. EUROPOS SĄJUNGOS
Microsoft Word - KLOM.doc
 Aptarnavimo instrukcija Valdymas ir duomenų vaizdavimas Pagrindinis jungiklis Pagrindinis jungiklis yra skirtas katilo įjungimui ar išjungimui. Jis yra katilo valdymo skydelyje (pozicija 6, pav. 1). Pirmąjį
Aptarnavimo instrukcija Valdymas ir duomenų vaizdavimas Pagrindinis jungiklis Pagrindinis jungiklis yra skirtas katilo įjungimui ar išjungimui. Jis yra katilo valdymo skydelyje (pozicija 6, pav. 1). Pirmąjį
PipeLife Stilla (LT)
 Pipelife Stilla Triukšmą slopinanti nuotekų sistema PPHT UAB Pipelife Lietuva yra koncerno Pipelife International GmbH dukterinė įmonė. Pipelife International GmbH koncerną įkūrė ir valdo dvi įmonės Wieneberger
Pipelife Stilla Triukšmą slopinanti nuotekų sistema PPHT UAB Pipelife Lietuva yra koncerno Pipelife International GmbH dukterinė įmonė. Pipelife International GmbH koncerną įkūrė ir valdo dvi įmonės Wieneberger
Nexa serija Stūmokliniai ir hidrauliniai dozavimo siurbliai su dviguba diafragma UAB Elega, Žalgirio , Vilnius, LT 08217, Lietuva, Tel:
 Nexa serija Stūmokliniai ir hidrauliniai dozavimo siurbliai su dviguba diafragma UAB Elega, Žalgirio 131-211, Vilnius, LT 08217, Lietuva, Tel: +370 5 2 715444; tel./faksas: +370 5 2 715445; mob. tel.:
Nexa serija Stūmokliniai ir hidrauliniai dozavimo siurbliai su dviguba diafragma UAB Elega, Žalgirio 131-211, Vilnius, LT 08217, Lietuva, Tel: +370 5 2 715444; tel./faksas: +370 5 2 715445; mob. tel.:
VANDENS SIURBLIAI, UAB Įmonės kodas PVM kodas LT Girulių g. 24, Šiauliai LT78138, Lietuva VANDENS JONIZATORIUS MIRACLE APR
 VANDENS SIURBLIAI, UAB Įmonės kodas 144708571 PVM kodas LT447085716 Girulių g. 24, Šiauliai LT78138, Lietuva VANDENS JONIZATORIUS MIRACLE - 1068.7 APRAŠYMAS: Jonizuotas vanduo yra labai artimas pačiam
VANDENS SIURBLIAI, UAB Įmonės kodas 144708571 PVM kodas LT447085716 Girulių g. 24, Šiauliai LT78138, Lietuva VANDENS JONIZATORIUS MIRACLE - 1068.7 APRAŠYMAS: Jonizuotas vanduo yra labai artimas pačiam
Slide 1
 Duomenų struktūros ir algoritmai 1 paskaita 2019-02-06 Kontaktai Martynas Sabaliauskas (VU MIF DMSTI) El. paštas: akatasis@gmail.com arba martynas.sabaliauskas@mii.vu.lt Rėmai mokykloje Rėmai aukštojoje
Duomenų struktūros ir algoritmai 1 paskaita 2019-02-06 Kontaktai Martynas Sabaliauskas (VU MIF DMSTI) El. paštas: akatasis@gmail.com arba martynas.sabaliauskas@mii.vu.lt Rėmai mokykloje Rėmai aukštojoje
Bioness
 Inovatyvus Bioness (FES) poveikis judėjimui po insulto Bioness kompetencijų centras UAB Vilniaus sveikatos namai Saulius Eidukevičius klinikinis instruktorius 2004 m. Izraelio ir JAV specialistų jungtinė
Inovatyvus Bioness (FES) poveikis judėjimui po insulto Bioness kompetencijų centras UAB Vilniaus sveikatos namai Saulius Eidukevičius klinikinis instruktorius 2004 m. Izraelio ir JAV specialistų jungtinė
EUROPOS KOMISIJA Briuselis, C(2018) 8589 final ANNEX 1 PRIEDAS prie Komisijos įgyvendinimo reglamento dėl duomenų patikros ir tikrintojų ak
 EUROPOS KOMISIJA Briuselis, 2018 12 19 C(2018) 8589 final ANNEX 1 PRIEDAS prie Komisijos įgyvendinimo reglamento dėl duomenų patikros ir tikrintojų akreditavimo pagal Europos Parlamento ir Tarybos direktyvą
EUROPOS KOMISIJA Briuselis, 2018 12 19 C(2018) 8589 final ANNEX 1 PRIEDAS prie Komisijos įgyvendinimo reglamento dėl duomenų patikros ir tikrintojų akreditavimo pagal Europos Parlamento ir Tarybos direktyvą
III. SVEIKI NENEIGIAMI SKAIČIAI 3.1 Indukcijos aksioma Natūraliu ju skaičiu aibės sa voka viena svarbiausiu matematikoje. Nors natūralaus skaičiaus sa
 III SVEIKI NENEIGIAMI SKAIČIAI 31 Indukcijos aksioma Natūraliu aibės sa voka viena svarbiausiu matematikoje Nors natūralaus skaičiaus sa voka labai sena, bet šio skaičiaus buveinės sa voka buvo suformuluota
III SVEIKI NENEIGIAMI SKAIČIAI 31 Indukcijos aksioma Natūraliu aibės sa voka viena svarbiausiu matematikoje Nors natūralaus skaičiaus sa voka labai sena, bet šio skaičiaus buveinės sa voka buvo suformuluota
KOMISIJOS REGLAMENTAS (ES) 2017/ m. balandžio 28 d. - kuriuo iš dalies keičiamas ir taisomas Reglamentas (ES) Nr. 10/
 L 113/18 2017 4 29 KOMISIJOS REGLAMENTAS (ES) 2017/752 2017 m. balandžio 28 d. kuriuo iš dalies keičiamas ir taisomas Reglamentas (ES) Nr. 10/2011 dėl plastikinių medžiagų ir gaminių, skirtų liestis su
L 113/18 2017 4 29 KOMISIJOS REGLAMENTAS (ES) 2017/752 2017 m. balandžio 28 d. kuriuo iš dalies keičiamas ir taisomas Reglamentas (ES) Nr. 10/2011 dėl plastikinių medžiagų ir gaminių, skirtų liestis su
