1 Vaizdu vidurkinimas ir požymiu išskyrimas 1.1 Glodus vienmatis eksponentinis filtras Apibrėšime eksponentini tolydu kintamojo x filtra formule ( v σ
|
|
|
- Aušra Gagys
- prieš 6 metus
- Peržiūrų:
Transkriptas
1 Vaizdu vidurkinimas ir požymiu išskyrimas. Glodus vienmatis eksponentinis filtras Apibrėšime eksponentini tolydu kintamojo x filtra formule ( v (x) = + x ) e x, x (, ). () Čia yra filtro parametras. Kad filtro reikšmės gestu begalybėje, reikalausime, kad > 0. Nesunku patikrinti, kad su bet kokia fiksuota parametro > 0 reikšme filtras yra du kartus tolydžiai diferencijuojamas atžvilgiu kintamojo x. Todėl ši filtra vadinsime glodžiu eksponentiniu filtru. Bet kokiam signalui u = u(x), filtravimo operacija apibrėžiama formule (u v )(x) = u(y)v (x y)dy = v (y)u(x y)dy. (2) Skaitmeniniu signalu atveju laikoma, kad u(x) = u n δ(x n), (3) n= kur δ = δ(x) yra delta-dirako funkcija pasižyminti savybe δ(y)φ(y)dy = φ(0) (4) visoms glodžioms integruojamoms funkcijoms φ = φ(x).pasinaudojȩ (3) ir (4) lygybėmis, gauname tokia filtravimo operacijos išraiška : (u v ) n = u m v (n m) = v (m)u n m, n = 0, ±, ±2,. (5) Atlikime filtravimo operacija vienetiniam skaitmeniniam signalui, t. y. signalui u(x) = n= δ(x n). Pasinaudoje filtravimo formulȩ, visiems sveikiesiems n, gausime (u v ) n = v (n m) = v (m) = ( + m m )e.
2 Pritaikȩ geometrinės progresijos sumos formulȩ rasime e m + e =. e Kadangi tai galutinai gauname me mt = ( e mt ) t = e t ( e t ) 2, (u v ) n = ( + m m )e ( e 2 ) + 2e = = ( e ) 2 q(). (6) Modifikuosime glodaus eksponentinio filtro apibrėžima taip, kad jo atsakas i vienetini skaitmenini signala būtu lygus. Kad tai pasiekti pakanka () dešinia ja pusȩ padauginti iš normuojančio daugikli q() apibrėžto formule (6). Tokiu būdu gauname tokia normuota eksponentinio filtro išraiška : v (x) = ( e ) 2 ( e 2 ) + 2e ( + x ) e x, x (, ). (7) Keičiant eksponentinio filtro parametra galima pasiekti norima signalo vidurkinimo lygi. Kuo arčiau nuliui, tuo filtravimo operacija mažiau glodina filtruojama signala ir atvirkščiai didinant parametro reikšmȩ didiname vidurkinimo laipsni. Išsiaiškinsime kaip efektyviai atlikti skaitmeninio signalo vidurkinima eksponentiniu filtru. Realiu skaitmeniniu signalu žinomu skaitmeniniu reikšmiu kiekis būna baigtinis. Tarkime žinome u 0, u, u 2,, u N reikšmes. Laikysime, kad filtruojamo signalo kraštinės reikšmės u 0 ir u N pratȩstos tolydžiai, t. y. ir u n u 0, kai n < 0 u n u N, kai n N. Kad supaprastinti formules, pradžioje nerašysime normuojančio daugiklio. Išskaidysime filtravimo operacijos suma i dvi dalis: (u v ) n = v (m)u n m = u n + ( + m )e m un m + 2 ( + m )e m un+m.
3 paveikslėlis: Glodžiu eksponentiniu filtru v grafikai. Mėlynas =, juodas = 2, žalias = 8 Užrašydami išskaidymo formulȩ pasinaudojome filtro simetriškumu, t. y. savybe v (x) = v ( x). Pradžioje raskime (u v0 + ) n = e m un m. (8) Kadangi visiems neigiamiems indeksams u n m = u 0, tai (u v0 + ) 0 = e u 0. Teigiamiems indeksams n > 0 galime užrašyti rekurentini ryši (u v0 + ) n = e (u v0 + ) n + u n. 3
4 Dabar apskaičiuokime (u v + ) n = me m un m. (9) Dėl kairiosios kraštinės sa lygos gauname (u v + ) 0 = e ( e ) u 0, 2 o teigiamiems indeksams n > 0 galime užrašyti sa ryši (u v + ) n = Analogiškai raskime me m un m = (m + )e m u n m = e ((u v + ) n + (u v0 + ) n ), n =, 2,, N. (0) (u v0 ) n = e m un+m. () Kadangi visiems indeksams m 0 u N +m = u N, tai (u v0 ) N = Likusiems indeksams n galime užrašyti sa ryši Liko apskaičiuoti e u N. (u v0 ) n = e (u v0 ) n+ + u n. (u v ) n = Dėl dešiniosios kraštinės sa lygos gauname me m un+m. (2) (u v ) N = e ( e ) 2 u N, o kitiems indeksams n 0 galioja sa ryšis (u v ) n = me m un+m = (m + )e m u n++m = e ((u v ) n+ + (u v0 ) n+ ), n = N 2, N 3,, 0. (3) Galutinės filtravimo formulės su normuojančiu daugikliu atrodo taip: (u v ) n = q()((u v0 + ) n + (u v+ ) n 4 + (u v0 ) n + (u v ) n u n ). (4)
5 .2 Filtruoto vienmačio signalo išvestinės Pateiktos formulės tinka pradinio skaitmeninio signalo greitam glodinimui. Kad apskaičiuoti v0 + n, v0 n, v + n ir v n reikia vienos daugybos ir vienos sudėties, o galutiniam normuotam filtravimo rezultatui gauti reikia atlikti dar dvi daugybas ir tris sudėties/atimties operacijas, taigi mūsu filtravimo algoritmo sudėtingumas yra 6 daugybos ir 7 sudėties operacijos vienam taškeliui. Tačiau praktikoje dažnai reikia ne tik suglodinti pradini signala bet ir i vertinti jo pirma ja ir antra ja išvestines. Išvestinės dažniausiai yra aproksimuojamos pirmosios ir antrosios eilės skirtumais. Tačiau mūsu atveju galima apskaičiuoti tiksliai filtruoto signalo išvestines. Formaliai diferencijuodami gauname (u v ) (x) = u(y)v (x y)dy = q() 2 u(y)(x y)e x y dy. (5) Diskrečiu atveju tiksli filtruoto signalo išvestinės formulė su normuojančiu daugikliu atrodo taip: (u v ) n = q() 2 me m un m = q() 2 ((u v + ) n (u v ) n ). (6) Iš (6) formulės matome, kad išsaugojus tarpinius glodinimo filtravimo rezultatus, išvestines apskaičiavimo papildomos sa naudos yra minimalios, tiksliau, kad apskaičiuoti filtruoto skaitmeninio signalo išvestinȩ viename taškelyje n reikia atlikti viena sudėties ir daugybos operacija. Analogiškai rasime tikslia antrosios eilės išvestinės formulȩ. Formaliai diferencijuodami du kartus filtravimo rezultata, gauname (u v ) (x) = u(y)v (x y)dy = q() 2 u(y)( x y )e x y dy. (7) Diskrečiu atveju filtruoto signalo antrosios eilės išvestinės formulė yra tokia: (u v ) n = q() 2 ( m m )e un m = q() 2 ((u v0 + ) n (u v+ ) n + (u v0 ) n (u v ) n u n ). (8) Taigi vėl gauname ekonomiška tikslu antrosios eilės išvestinės apskaičiavimo algoritma, kurio sudėtingumas yra 2 daugybos ir 4 sudėties/atimties operacijos. 5
6 Reikia pastebėti, kad jei mūsu filtras nebūtu du kartu tolydžiai diferencijuodamas, tai formalus išvestiniu i kėlimas po konvoliucijos (filtravimo) integralu ženklu duotu klaidingas formules. Tačiau net ir su glodžiu filtru gauname, kad konstantos antrosios eilės išvestinė yra nenulinė, o etaloniniu signalu u n = n ir u n = n 2 vidurkintos reikšmės ir ju išvestinės tiksliai nesutampa su laukiamomis reikšmėmis. Kad ištaisyti šias filtru ydas, reikalausime, kad visi filtrai būtu apskaičiuotu pagal (8), (9), ir 2 išraiškas funkciju tiesiniai dariniai, vidurkintas signalas nekeistu vienetini (u n = )ir kvadratini (u n = n 2 ) signalus, tiesinio signalo (u n = n) išvestinė būtu lygi vienetiniam signalui ir ir kvadratinio signalo u n = n 2 išvestinė būtu lygi konstantai 2. Pagal šias sa lygas gauname tokias galutines formules: kur u n = a 0 ((u v0 ) n u n ) + b 0 (u v ) n, (vidurkintas signalas) (9) u n = a (u v + ) n + b (u v ) n, (vidurkinto signalo išvestinė) (20) u n = a 2 ((u v0 ) n u n ) + b 2 (u v ) n, (antrosios eilės išvestinė), (2) v0 n = v0 + n + v0 n, (22) v n = v + n + v n, (23) q 0 () = = ( + e )/( e ), (24) q () = q 2 () = q 3 () = e m m e m m 2 e m m 3 e m = 2 e /( e ) 2, (25) = 2e ( + e )/( e ) 3, (26) = 2e ( + 4 e + e 2 )/( e ) 4, (27) 6
7 o daugikliai a ir b randami iš lygčiu a 0 q 0 () + b 0 q () =, (28) a 0 q 2 () + b 0 q 3 () = 0, (29) a q 2 () + b 0 =, (30) a 0 + b q 2 () =, (3) a 2 q 0 () + b 2 q () = 0, (32) a 2 q 2 () + b 2 q 3 () = 2.. (33) Alternatyvus koeficentu a 0 ir b 0 apibrėžimo variantas: a 0 = b 0 = a 2 a 2 q 0 b 2 q, (34) b 2 a 2 q 0 b 2 q. (35) Skaičiuojant a 0 ir b 0 pagal šias formules vidurkinta konstanta išlieka ta pačia konstanta ir išlaikoma simetrija: a 0 = const a 2, b 0 = const b Praktinė vienmačiu signalu vidurkinimo užduotis Parašyti programa, kuri apskaičiuotu duoto skaitmeninio signalo suglodinima eksponentiniu filtru ir rastu suglodinto signalo pirma sias ir antra sias išvestines. Algoritmo testavimui imkite tokius duomenis:, kai n < 00, u n = 3, kai n < 200, 2, kai n < 300, = 2. Dumenys kiekvieno algoritmo žingsnio testavimui: = log 2, u = , (u v0 + ) = , (u v + ) = , (u v0 ) = , (u v ) =
8 a 0 = 3 27, b 0 = 9, a = 2, b = 2 a 2 = 2 27, b 2 = 8. u = , u = , u = , u = Atlikite filtravima etaloniniams duomenis u n =, u n = n ir u n = n 2 ir pakomentuokite gautus filtravimo rezultatus. Šioje ir kitose programose nebūtina realizuoti vartotojo grafinȩ sa saja. Vertinama iki 0.75 egzamino balu. Jei dėl nepateisinamu priežasčiu atsiskaitoma vėliau nei keturios savaitės nuo pirmu ju pratybu, už kiekvienos savaitės vėlavima vertinimas mažinamas 0.25 balo..3 Vaizdu vidurkinimas ir gradiento i vertis Apibendrinsime vienmačiu signalu eksponentini vidurkimo filtra () dvimačiams vaizdams: ( v (x, y) = + x ) ( + y ) e x + y, x, y (, ). (36) Nesunku pastebėti, kas dvimatis filtras yra vienmačiu filtru sandauga, t. y. v (x, y) = v (x)v (y). Ši filtro savybė lemia, kad dvimatis filtravimas gali būti atliktas pirma vaizdo eilutėms taikant eksponentini filtravima, o vėliau gautam filtruotam vaizdui atliekamas eksponentinis filtravimas stulpeliams. Lygiai ta pati rezultata galima pirma atliekant filtravima vaizdo stulpeliams, o paskui eilutėms. Matematiškai ši savybė ekvivalenti teiginiui, kad kartotinio integralo reikšmė nepriklauso nuo integravimo tvarkos, jei integruojama funkcija yra pakankamai gera. Koks yra sa vokos pakankamai gera tikslus matematinis turinys mes netikslinsime, nes realaus pasaulio analoginiai vaizdai yra tolydūs, mūsu filtrai taip pat tolydūs, tai tolydžios funkcijos (vaizdo) ir tolydaus filtro sandauga taip pat yra tolydi funkcija ir tokios kartotinio integralo reikšmės nepriklauso nuo integravimo tvarkos. Todėl diskrečiu atveju vidurkinant vaizda reikia pritaikyti (9) filtra eilutėms, o po to pritaikyti ta pati filtra gautam vidurkintam 8
9 vaizdui. Atliekant šias operacijas galima naudoti skirtingu filtrus, bet dėl filtro simetriškumo prasminga naudoti ta pačia. 2 paveikslėlyje iliustruoti pradini rainelės vaizda, jo vidurkinta, gradiento ir Laplaso vaizdus. Kad gradiento ir Laplaso vaizdai būtu labiau informatyvūs, iš gautu vaidu modulio buvo ištraukta kvadratinė šaknis ir padauginta iš ženklo. Vidurkinimo skalės parametro reikšmė = 3. Kaip gaunamas vidurkintas vaizdas mes jau išsiaiškinome. Gradiento vaizdas žymi vidurkinto vaizdo gradiento moduli, t. y. u = ( u x )2 + ( u y )2, (37) o vidurkinto vaizdo Laplasas randamas pagal tokia taisyklȩ: u = 2 u x u y 2. (38) Kadangi Laplaso vaizdo reikšmės gali būti neigiamos ir teigiamos, teigiamos reikšmės vaizduojamos raudonai, neigiamos mėlynai. Kad rasti vaizdo išvestines x kryptimi, reikia taikyti (20) ir (2) taisykles eilutėms ir (9) taisyklȩ stulpeliams. Vidurkinto vaizdo išvestinės y kryptimi randamos taikant (20) ir (2) taisykles stulpeliams ir (9) taisyklȩ eilutėms. Kadangi pratybu metu vėlesnėse užduotyse pasirinktinai lyginsite pirštu atspaudus, veidus arba raineles, pateiksime ir veido bei raineliu vidurkintu vaizdu pavyzdžius. Iš pateiktu vidurkinto veido, gradiento ir Laplaso vaizdu matyti, kad ir gradientas ir Laplaso vaizdai atrodo estetiškai, todėl yra prasminga iš ju išskirti požymius. Vidurkinti piršto atspaudo gradiento ir Laplaso vaizdai atrodo neestetiškai, nes susidaro i spūdis, kad piršto atspaudo liniju tankis yra padvigubėjȩs du kartus. Todėl vėliau išskiriant požymius rekomenduojama naudoti tik vidurkinta piršto atspauda arba Laplaso vaizde išskirti apibendrintus minimumo ir maksimumo taškus..3. Dvimačio vidurkinimo praktinė užduotis Parašyti programa, kuri apskaičiuotu duoto skaitmeninio vaizdo suglodinima eksponentiniu simetriniu filtru ir rastu suglodinto vaizdo gradiento modulio ir Laplaso vaizdus. Algoritmo testavimui imkite = 3 ir tokius vaizdus: 9
10 2 paveikslėlis: Casia duomenu bazės pirmosios rainelės pradinis vaizdas (kairėje viršuje), jos vidurkintas analogas (dešinėje viršuje, = 3, vidurkinto vaizdo gradiento modulis (kairėje apačioje) ir vidurkinto vaizdo Laplasas (dešinėje apačioje) Casia DB pirmoji rainelė figures/00.bmp Ferret grey DB pirmasis veidas figures/0000da png FVC 2000 DB pirmasis piršto atspaudas figures/.tif Jei kyla problemu su kokio nors formato duomenu nuskaitymu, galite juos konvertuoti i jums patogu formata panaudojant ir pan. priemones.. Kontroliniu vaizdu apdorojimo rezultatus galite palyginti su šiu konspektu iliustracijomis; turi gautis vaizdai panašūs i 2-4 paveikslėliu vaizdus. Vertinama iki 0.75 egzamino balu. Jei dėl nepateisinamu priežasčiu atsiskaitoma vėliau nei penkios savaitės nuo pirmu ju pratybu, už kiekvienos savaitės vėlavima vertinimas mažinamas 0.25 balo..4 Vaizdu požymiai Vaizdu požymiams i vertinti naudosime gradiento modulio apibendrintus lokalius ekstremumus ir Laplaso nulio kirtimus []. Abudu šie požymiai apytikriai išskiria 0
11 3 paveikslėlis: Ferret duomenu bazės veido pradinis vaizdas (kairėje viršuje), jo vidurkintas analogas (dešinėje viršuje, = 3, vidurkinto vaizdo gradiento modulis (kairėje apačioje) ir vidurkinto vaizdo Laplasas (dešinėje apačioje) vaizdo objektu kontūrus. Tačiau dėl išvestiniu nestabilumo dalis gaunamu kontūru neturi aiškios interpretacijos. Kad sumažinti tokiu kontūru skaičiu galima didinti vidurkinimo mastelio vertȩ. Tačiau toks būdas mažina realiu kontūru padėties nustatymo tiksluma. Kitas būdas derinti gradiento apibendrintu lokaliu maksimumu ir Laplaso nulio kirtimu kontūrus. Jei ir vienu ir kitu būdu gaunami greta du tokie kontūrai, tai labai padidina tikimybȩ, kad jie atitinka realu kontūra. Dar vienas būdas yra derinti kontūrus gautus vidurkinant vaizda su keliais skirtingais. Čia vėl yra ieškomi artimi keliuose vidurkintuose vaizduose kontūrai, tačiau tiksliai apibrėžti kontūru artumo sa voka gana keblu. Gana neblogai ir paprastai netikri kontūrai eliminuojami pasirenkant slenksti ir ignoruojant kontūrus, kuriu gradiento
12 4 paveikslėlis: FVC 2000 DB duomenu bazės pirmojo piršto atspaudo pradinis vaizdas (kairėje viršuje), jo vidurkintas analogas (dešinėje viršuje, = 3, vidurkinto vaizdo gradiento modulis (kairėje apačioje) ir vidurkinto vaizdo Laplasas (dešinėje apačioje) modulio reikšmės mažesnės už slenksti ir eliminuojant trumpus kontūrus. Tačiau ir vienu ir kitu atveju reikia turėti slenksti nusakanti gradiento arba kontūro ilgio mažuma, o tai menkina tokio būdo vertȩ. Kokiu būdu išskirti gradientiniame arba Laplaso vaizde kontūrus? Pradėsime nuo Laplaso vaizdo, kadangi jame kontūrai išskiriami remiantis paprastu nuliu kirtimo principu, kuris pažymi diskrečias pozicijas, kuriu kaimynystėje Laplasas lygus nuliui. Labai maža tikimybė, kad kokioje nors diskrečioje pozicijoje Laplasas bus tiksliai lygus nuliui. Tačiau kadangi Laplaso vaizde matome ir raudonas teigiamo ženklo zonas ir mėlynas neigiamo ženklo zonas, tai aišku, kad atsiras ju jungimosi taškus. Paprasčiausias būdas rasti tokius taškus yra fiksuoti pozicija (m, n) ir patikrinti sa lyga u m,n+ u m,n 0 u m+,n u m,n 0. 2
13 Jei Laplaso vaizde randame toki taškeli, ji pažymime tarkime baltai, likusius žymime juodai. Kiek sunkiau i vertinti gradiento apibendrintus ekstremumus. Jei žymėtume tik tikrus gradiento ekstremumus, tai pažymėtu tašku vaizde atsirastu tik pavieniai pažymėti taškai ir negautumėme kontūru. Todėl i vesime sa voka apibendrinto ekstremumo. apibrėžimas. Fiksuokime spinduli R > 0 ir pozicija (x, y). Tarkime taškelio skritulinėje aplinkoje yra C diskrečiu poziciju nutolusiu ne daugiau kaip per atstuma R. Fiksuokime diskretu ji vaizda u = u x,y ir tegul c skritulinės aplinkos taškeliuose vaizdo reikšmės viršija vaizdo reikšmȩ centriniame taške. Tuomet sakysime, kad (x, y) yra diskretaus vaizdo u x,y c-osios eilės apibendrinto maksimumo taškas, jei c <= C/2. Jei c > C/2., toki taškeli Vadinsime (C c)-osios eilės apibendrintas minimumo tašku. Pagal pateikta apibrėžima kiekvienas taškelis yra apibendrintas kokios nors eilės maksimumo arba minimumo taškeliu. Apibrėžiant kontūra mes paliksime tik ekstremumu taškelius, kuriu eilė yra nedidesnė už pasirinkta parametra. Rekomenduojama fiksuoti R = 3 ir pažymėti visus apibendrintus ekstremumus, kuriu eilė nedidesni už 0. Tačiau jūs esate laisvi eksperimentuoti ir pasirinkti savo parametrus. Apibendrintus maksimumo taškelius žymėsime raudonai, o minimumo taškelius mėlynai. Tokiu būdu gausime dvieju spalvu kontūru vaizdeli. 5 paveikslėlis iliustruoja raineles vidurkinto ir gradiento vaizduose išskirtus kontūrus, kurie sudaryti iš apibendrintu ju ekstremumu. Vidurkintame vaizde raudonai nuspalvinti apibendrinti lokalaus maksimumo taškai, o mėlynai minimumo taškai. Visais atvejais išskiriant reikšmingus apibendrintus lokaliuosius ekstremumus ėmėme R = 3 ir lokalius ekstremumus, kuriu eilė nedidesnė kaip 0 (c <= 0). Taip pat pateiktas dar vienas kontūru paveikslėlis gautas pažymint baltai Laplaso nulio kirtimo taškus..4. Skaitmeninio vaizdo kontūru išskyrimo praktinė užduotis Parašyti programa, kuri apskaičiuotu duoto skaitmeninio vaizdo kontūrus. Pirma suglodinkite vaizda eksponentiniu simetriniu filtru ir raskite jo gradiento modulio ir Laplaso vaizdus (pereita praktinė užduotis). Toliau vidurkintame išskirkite apibendrintus ekstremumus, gradientiniame vaizde apibendrintus lokalius maksimumus, 3
14 5 paveikslėlis: Vidurkintos rainelės apibendrinti lokalūs ekstremumai (kairėje viršuje), jos gradiento apibendrinti lokalūs maksimumai (dešinėje viršuje), Laplaso nulio kirtimai (apačioje) 6 paveikslėlis: Vidurkinto veido apibendrinti lokalūs ekstremumai (kairėje ), jo gradiento apibendrinti lokalūs maksimumai (viduryje), Laplaso nulio kirtimai (dešinėje) 4
15 7 paveikslėlis: Vidurkinto piršto apibendrinti lokalūs ekstremumai (kairėje ), jo gradiento apibendrinti lokalūs maksimumai (viduryje), Laplaso nulio kirtimai (dešinėje) o Laplaso vaizde nulio kirtimus. Glodinimo parametra, aplinkos spinduli R ir ekstremumu eilȩ C pasirinkite laisvai optimizuodami gautu kontūru estetini vaizda. Išskiriant kontūrus eksperimentuokite su pereitos užduoties vaizdais. Pasistenkite gauti vaizdus panašius i 5-4 pateiktuose paveikslėliuose gautus kontūrus. Vertinama iki 0.75 egzamino balu. Jei dėl nepateisinamu priežasčiu atsiskaitoma vėliau nei devynios savaitės nuo pirmu ju pratybu, už kiekvienos savaitės vėlavima vertinimas mažinamas 0.25 balo..5 Vaizdu požymiu mažinimas ir papildomi atributai Gautus skaitmeninio vaizdo kontūru taškus laikysime jo požymiais. Išskiriant požymius siekiama mažinti ju kieki atmetant mažai informatyvius ir pridedant atributus, didinančius požymiu informatyvuma. Intuityviai aišku, kad gautus kontūrus, sudarytus iš požymiu tašku, galima suploninti iki vieno taškelio storio praktiškai nesumažinant kontūru taškais perteikiamos informacijos. Storu kontūru, ar plotu ploninimas iki vieno taškelio storio jungiu taku liniju vadinamas skeletizavimu [2]. Šiame kurse nesigilinsime ir nesieksime realizuoti kokio nors skeletizavimo algoritmo, o pasinaudosime jūsu kolegu skeletizavimo algoritmu kokia nors realizacija [3]. Turint skeletizuota vaizda, galima nutrinti labai trumpus jungius kontūrus, išskirti kontūru ypatingus taškus, kurie charakterizuoja liniju išsidėstyma ir ju jungimosi topologija. Paprasčiausias būdas išskirti ypatingus plonu liniju taškus yra fiksuoti linijos taškeli ir ieškoti kiek kartu jo aštuoniu kaimynu aplinkoje pereinama iš baltos 5
16 lentelė: Nepatogiu ypatingu tašku klasifikacijai atveju pavyzdžiai i juoda arba atvirkščiai. Suradus ši skaičiu, jis dalinamas iš dvieju ir gauta vertė K charakterizuoja linijos taška. Šis metodas kartais vadinamas straipsnio autoriaus, kuris pirmasis ji paskelbė, Rutovič vardu [4]. Žemiau pateiktoje lentelėje nurodytos galimos K reikšmės ir jos interpretacijos. K Taško interpretacija 0 Pavienis Pabaiga 2 Jungumo (neypatingas) 3 Išsišakojimo 4 Susikryžiavimo Matematiškai tai galima užrašyti taip: u 6 u 7 u 8 u 5 u 0 u K = 8 2 i= u i u i+, kur u 9 = u ir u i u i+ = 0, kai reikšmės u 4 u 3 u 2 sutampa, ir u i u i+ = priešingu atveju. Deja šis paprastas ypatingu tašku klasifikacijos būdas kartais duoda nenatūralius rezultatus. ]reftab:blogiatvejai lentelėje pateikta keletas pavyzdžiu. Pasvirȩ 0 ir taškeliai žymi pozicijas, kuriose gaunami nenatūralūs ypatingieji taškai. Tokiu tašku eliminavimui taikomi papildomi vaizdu apdorojimo metodai [5]. Paliekant tolimesniam atpažinimui naudoti tik išskirtus ypatinguosius taškus ženkliai sumažiname požymiu kieki. Taip labai dažnai daroma pirštu atspaudu vaizdu palyginime. Tačiau net ir pirštu atspaudu atveju nepakanka vien tik informacijos apie ypatingojo taško tipa ir jo koordinates. Gana dažnai naudojami papildomi kontūro tašku atributai, kurie pagerina atpažinimo kokybȩ. Tarkime kontūras yra 6
17 sudarytas iš gradiento modulio apibendrintu ju maksimumo tašku. Tokiuose taškuose gana patikimai i vertinama gradiento kryptis ir jos kvantuota vertȩ galima laikyti papildomu požymio atributu. 8-0 paveikslėliai iliustruoja suplonintus gradientu 8 paveikslėlis: Rainelės gradiento modulio požymiai su krypties atributu ( = 2) kontūrus, kurie sudaryti iš apibendrintu ju maksimumu. Gaunant šiuos vaizdus, vidurkinant buvo naudoti (34) ir (35) formulėmis apskaičiuojami koeficientai a 0 ir b 0, o vertės buvo parenkamos individualiai kiekvienam paveikslėlio tipui. Apibendrintu ju maksimumu kontūrai buvo suploninti panaudojant skeletizavimo algoritma [6]. Suplonintu kontūru taškai nuspalvinti remiantis gradiento kryptimi. Gradiento vektorius yra sudarytas iš vidurkinto vaizdo išvestiniu x ir y kryptimis. Šias išvestines anksčiau naudojome apskaičiuojant gradiento modulio(37) reikšmes. Spalvos kvantuojamos aštuoniomis lygiomis dalimis iš galimu gradiento vektoriaus polinio kampo reikšmiu. Spalvu tvarka pagal laikrodžio rodyklȩ: RED, GREEN, BLUE, WHITE, YELLOW, CYAN, MAGENTA, GREY; pirma raudona spalva žymi kryptis, kurios sudaro su horizonto kryptimi kampa α nuo π/8 iki π/8. Gradiento kampas su horizonto ašimi surandamas pagal formulȩ α = atan2(u y (x, y), u x (x, y)). 7
18 9 paveikslėlis: Veido gradiento modulio požymiai su krypties atributu ( = 3) Čia atan2 = atan2(y, x) dvieju argumentu funkcija, kuri taško Dekarto koordinatėms (x,y) gra žina polinio kampo reikšmȩ. Ši funkcija yra realizuota visose programavimo kalbose; ja naudojantis atkreipkite dėmesi, kad kreipiantis reikia sukeisti Dekarto koordinačiu tvarka..5. Raineliu, veidu ir pirštu atspaudu vieningu požymiu išskyrimo praktinė užduotis Parašyti programa, kuri apskaičiuotu duoto skaitmeninio vaizdo suplonintus apibendrintu gradiento modulio maksimumu kontūrus. Kontūrus nuspalvinkite pagal kvantuotas aštuonias gradiento kryptis. Skaičiavimas naudokite ankstesnės užduoties programa. Vidurkinimo parametra parinkite savo nuožiūra individualiai kiekvieno tipo vaizdui, kad gautu si estetiškesnis galutiniu požymiu vaizdas. 8
19 0 paveikslėlis: Piršto atspaudo požymiai su krypties atributu ( = ) Eksperimentuokite su pereitos užduoties vaizdais. Pasistenkite gauti vaizdus panašius i 8-0 paveikslėliuose gautus rainelės, veido ir piršto atspaudo požymiu vaizdus. Vertinama iki 0.75 egzamino balu. Jei dėl nepateisinamu priežasčiu atsiskaitoma vėliau nei devynios savaitės nuo pirmu ju pratybu, už kiekvienos savaitės vėlavima vertinimas mažinamas 0.25 balo. Literatūra [] Bill Green, weg22/edge.html [2] Kálmán Palágyi, Vengrija, palagyi/skel/skel.html [3] K. Stukas, J. Janauskas, Š. Gruodis, M. Brašiškis, bastys/academic/ate/skaiciai/skaiciu atp.htm#praktinis [4] D. Rutovitz, Pattern Recognition, J. Roy. Statist. Soc., vol. 29, pp ,
20 [5] Feng Zhao and Xiaoou Tang, CISST02 International Conference, Fingerprint.pdf, (Lokali kopija bastys/academic/ate/pirshtai/cisst02 Fingerprint.pdf) [6] T. Y. Zhang, C. Y. Suen, A fast parallel algorithm for thinning digital patterns, Communications of the ACM, v.27 n.3, p , March 984. Realizacija Java kalba: 20
LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 7. PAPRASČIAUSIOS DIFERENCIALINĖS LYGTYS ( ) Teorinę medžiagą parengė ir septintąją užduotį sudarė prof. d
 LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 7 PAPRASČIAUSIOS DIFERENIALINĖS LYGTYS (07 09) Teorinę medžiagą parengė ir septintąją užduotį sudarė prof dr Eugenijus Stankus Diferencialinės lygtys taikomos sprendžiant
LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 7 PAPRASČIAUSIOS DIFERENIALINĖS LYGTYS (07 09) Teorinę medžiagą parengė ir septintąją užduotį sudarė prof dr Eugenijus Stankus Diferencialinės lygtys taikomos sprendžiant
* # * # # 1 TIESĖS IR PLOKŠTUMOS 1 1 Tiesės ir plokštumos 1.1 Lygtys ir taškų aibės Sferos lygtis Tarkime, kad erdvėje apibrėžta Dekarto stačiak
 1 TIESĖS IR PLOKŠTUMOS 1 1 Tiesės ir plokštumos 1.1 Lygtys ir taškų aibės 1.1.1 Sferos lygtis Tarkime kad erdvėje apibrėžta Dekarto stačiakampė koordinačių sistema Sfera su centru taške ir spinduliu yra
1 TIESĖS IR PLOKŠTUMOS 1 1 Tiesės ir plokštumos 1.1 Lygtys ir taškų aibės 1.1.1 Sferos lygtis Tarkime kad erdvėje apibrėžta Dekarto stačiakampė koordinačių sistema Sfera su centru taške ir spinduliu yra
MatricosDetermTiesLS.dvi
 MATRICOS Matricos. Pagrindiniai apibrėžimai a a 2... a n a 2 a 22... a 2n............ a m a m2... a mn = a ij m n matrica skaičių lentelė m eilučių skaičius n stulpelių skaičius a ij matricos elementas
MATRICOS Matricos. Pagrindiniai apibrėžimai a a 2... a n a 2 a 22... a 2n............ a m a m2... a mn = a ij m n matrica skaičių lentelė m eilučių skaičius n stulpelių skaičius a ij matricos elementas
TIESINĖ ALGEBRA Matricos ir determinantai Matricos. Transponuota matrica. Nulinė ir vienetinė matrica. Kvadratinė matrica. Antrosios ir trečiosios eil
 TIESINĖ ALGEBRA Matricos ir determinantai Matricos. Transponuota matrica. Nulinė ir vienetinė matrica. Kvadratinė matrica. Antrosios ir trečiosios eilės determinantai. Minorai ir adjunktai. Determinantų
TIESINĖ ALGEBRA Matricos ir determinantai Matricos. Transponuota matrica. Nulinė ir vienetinė matrica. Kvadratinė matrica. Antrosios ir trečiosios eilės determinantai. Minorai ir adjunktai. Determinantų
Lietuvos mokinių matematikos olimpiada Rajono (miesto) etapo užduočių klasei sprendimai 2015 m. 1 uždavinys. Aistė užrašė skaičių seką: 1 (2 3)
 Lietuvos mokinių matematikos olimpiada Rajono (miesto) etapo užduočių 11-12 klasei sprendimai 2015 m. 1 uždavinys. Aistė užrašė skaičių seką: 1 (2 3) 4, 4 (5 6) 7, 7 (8 9) 10,..., 2014 (2015 2016) 2017.
Lietuvos mokinių matematikos olimpiada Rajono (miesto) etapo užduočių 11-12 klasei sprendimai 2015 m. 1 uždavinys. Aistė užrašė skaičių seką: 1 (2 3) 4, 4 (5 6) 7, 7 (8 9) 10,..., 2014 (2015 2016) 2017.
Microsoft PowerPoint Ekstremumai_naujas
 Kelių kintamųjų funkcijos lokalūs ekstremumai. Ekstremumų egzistavimo būtina ir pakankama sąlygos. Sąlyginiai ekstremumai. Lagranžo daugikliai. Didžiausioji ir mažiausioji funkcijos reikšmės uždaroje srityje.
Kelių kintamųjų funkcijos lokalūs ekstremumai. Ekstremumų egzistavimo būtina ir pakankama sąlygos. Sąlyginiai ekstremumai. Lagranžo daugikliai. Didžiausioji ir mažiausioji funkcijos reikšmės uždaroje srityje.
Teorinių kontrolinių sąlygos ir sprendimai Vytautas Kazakevičius 2016 m. gruodžio 20 d. Teiginiai ( ). 1. (0.05 t.) Užrašykite formule tokį t
 Teorinių kontrolinių sąlygos sprendimai Vytautas Kazakevičius 206 m. gruodžio 20 d. Teiginiai (206-09-4).. (0.05 t.) Užrašykite formule tokį teiginį: jei iš dviejų teigiamų skaičių vienas yra mažesnis
Teorinių kontrolinių sąlygos sprendimai Vytautas Kazakevičius 206 m. gruodžio 20 d. Teiginiai (206-09-4).. (0.05 t.) Užrašykite formule tokį teiginį: jei iš dviejų teigiamų skaičių vienas yra mažesnis
4 skyrius Algoritmai grafuose 4.1. Grafų teorijos uždaviniai Grafai Tegul turime viršūnių aibę V = { v 1,v 2,...,v N } (angl. vertex) ir briaun
 skyrius Algoritmai grafuose.. Grafų teorijos uždaviniai... Grafai Tegul turime viršūnių aibę V = { v,v,...,v N (angl. vertex) ir briaunų aibę E = { e,e,...,e K, briauna (angl. edge) yra viršūnių pora ej
skyrius Algoritmai grafuose.. Grafų teorijos uždaviniai... Grafai Tegul turime viršūnių aibę V = { v,v,...,v N (angl. vertex) ir briaunų aibę E = { e,e,...,e K, briauna (angl. edge) yra viršūnių pora ej
PS_riba_tolydumas.dvi
 Funkcijos riba ir tolydumas Ribos apibrėžimas Nykstamosios funkcijos Funkcijos riba, kai x + Skaičių sekos riba Neaprėžtai didėjančios funkcijos Neapibrėžtumai Vienpusės ribos Funkcijos tolydumas Funkcijos
Funkcijos riba ir tolydumas Ribos apibrėžimas Nykstamosios funkcijos Funkcijos riba, kai x + Skaičių sekos riba Neaprėžtai didėjančios funkcijos Neapibrėžtumai Vienpusės ribos Funkcijos tolydumas Funkcijos
(Microsoft Word - Pasiruo\360imas EE 10 KD-1)
 -as kontrolinis darbas (KD-) Kompleksiniai skaičiai. Algebrinė kompleksinio skaičiaus forma Pagrindinės sąvokos apibrėžimai. Veiksmai su kompleksinio skaičiais. 2. Kompleksinio skaičiaus geometrinis vaizdavimas.
-as kontrolinis darbas (KD-) Kompleksiniai skaičiai. Algebrinė kompleksinio skaičiaus forma Pagrindinės sąvokos apibrėžimai. Veiksmai su kompleksinio skaičiais. 2. Kompleksinio skaičiaus geometrinis vaizdavimas.
9 paskaita 9.1 Erdvės su skaliarine daugyba Šiame skyriuje nagrinėsime abstrakčias tiesines erdves, kurioms apibrėžta skaliarinė daugyba. Jos sudaro l
 9 paskaita 9.1 Erdvės su skaliarine daugyba Šiame skyriuje nagrinėsime abstrakčias tiesines erdves, kurioms apibrėžta skaliarinė daugyba. Jos sudaro labai svarbu normuotu ju erdviu šeimos pošeimį. Pilnosios
9 paskaita 9.1 Erdvės su skaliarine daugyba Šiame skyriuje nagrinėsime abstrakčias tiesines erdves, kurioms apibrėžta skaliarinė daugyba. Jos sudaro labai svarbu normuotu ju erdviu šeimos pošeimį. Pilnosios
10 Pratybos Oleg Lukašonok 1
 10 Pratybos Oleg Lukašonok 1 2 Tikimybių pratybos 1 Lema Lema 1. Tegul {Ω, A, P} yra tikimybinė erdvė. Jeigu A n A, n N, tai i) P (lim sup A n ) = P ( k=1 n=k A n ) = lim P ( n k n=ka n ), nes n=ka n monotoniškai
10 Pratybos Oleg Lukašonok 1 2 Tikimybių pratybos 1 Lema Lema 1. Tegul {Ω, A, P} yra tikimybinė erdvė. Jeigu A n A, n N, tai i) P (lim sup A n ) = P ( k=1 n=k A n ) = lim P ( n k n=ka n ), nes n=ka n monotoniškai
Isvestiniu_taikymai.dvi
 IŠVESTINIŲ TAIKYMAI Pagrindinės analizės teoremos Monotoninės funkcijos išvestinė Funkcijos ekstremumai Funkcijos didžiausia ir mažiausia reikšmės intervale Kreivės iškilumas Funkcijos grafiko asimptotės
IŠVESTINIŲ TAIKYMAI Pagrindinės analizės teoremos Monotoninės funkcijos išvestinė Funkcijos ekstremumai Funkcijos didžiausia ir mažiausia reikšmės intervale Kreivės iškilumas Funkcijos grafiko asimptotės
PowerPoint Presentation
 Algoritmai ir duomenų struktūros (ADS) 13 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2018-05-14 Šaltinis Paskaita parengta pagal William Pugh Skip Lists: A Probabilistic Alternative to
Algoritmai ir duomenų struktūros (ADS) 13 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2018-05-14 Šaltinis Paskaita parengta pagal William Pugh Skip Lists: A Probabilistic Alternative to
Algebra ir geometrija informatikams. Paskaitu¾ konspektas Rimantas Grigutis 7 paskaita Matricos. 7.1 Apibr eµzimas. Matrica A yra m eiluµciu¾ir n stul
 lgebra ir geometrija informatikams. Paskaitu¾ konspektas Rimantas Grigutis 7 paskaita Matricos. 7. pibr eµzimas. Matrica yra m eiluµciu¾ir n stulpeliu¾turinti staµciakamp e lentel e su joje i¾rašytais
lgebra ir geometrija informatikams. Paskaitu¾ konspektas Rimantas Grigutis 7 paskaita Matricos. 7. pibr eµzimas. Matrica yra m eiluµciu¾ir n stulpeliu¾turinti staµciakamp e lentel e su joje i¾rašytais
VI. TOLYDŽIU IR DIFERENCIJUOJAMU FUNKCIJU TEOREMOS 6.1 Teoremos apie tolydžiu funkciju tarpines reikšmes Skaitytojui priminsime, kad nagrinėdami reali
 VI TOLYDŽIU IR DIFERENCIJUOJAMU FUNKCIJU TEOREMOS 61 Teoremos apie tolydžiu tarpines reikšmes Skaitytojui priminsime, kad nagrinėdami realiu ju skaičiu savybes atkreipėme dėmesi i tokia šios aibės elementu
VI TOLYDŽIU IR DIFERENCIJUOJAMU FUNKCIJU TEOREMOS 61 Teoremos apie tolydžiu tarpines reikšmes Skaitytojui priminsime, kad nagrinėdami realiu ju skaičiu savybes atkreipėme dėmesi i tokia šios aibės elementu
Slide 1
 Duomenų struktūros ir algoritmai 1 paskaita 2019-02-06 Kontaktai Martynas Sabaliauskas (VU MIF DMSTI) El. paštas: akatasis@gmail.com arba martynas.sabaliauskas@mii.vu.lt Rėmai mokykloje Rėmai aukštojoje
Duomenų struktūros ir algoritmai 1 paskaita 2019-02-06 Kontaktai Martynas Sabaliauskas (VU MIF DMSTI) El. paštas: akatasis@gmail.com arba martynas.sabaliauskas@mii.vu.lt Rėmai mokykloje Rėmai aukštojoje
PowerPoint Presentation
 Algoritmai ir duomenų struktūros (ADS) 15 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2018-05-28 Grįžtamasis ryšys Ačiū visiems dalyvavusiems Daug pagyrimų Ačiū, bet jie nepadeda tobulėti.
Algoritmai ir duomenų struktūros (ADS) 15 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2018-05-28 Grįžtamasis ryšys Ačiū visiems dalyvavusiems Daug pagyrimų Ačiū, bet jie nepadeda tobulėti.
TAIKOMOJI MATEMATIKA IR KIEKYBINIAI METODAI. Rašto darbas serija 3081 variantas Nustatykite funkcijos f(x) = x+2 x 6 cos ( 3x) apibrėžimo sritį.
 00 Nustatykite funkcijos f() = +2 6 cos ( 3) apibrėžimo sritį (, 0) (0, 2) (2, + ) 2 (, 2) ( 2, + ) 3 (, 2] 4 [ 2, + ) 5 [2, ) 6 (, 2] 7 (, + ) 8 [ 2, 0) (0, + ) 0 (, 2) (2, + ) { a + b, kai 7, Raskite
00 Nustatykite funkcijos f() = +2 6 cos ( 3) apibrėžimo sritį (, 0) (0, 2) (2, + ) 2 (, 2) ( 2, + ) 3 (, 2] 4 [ 2, + ) 5 [2, ) 6 (, 2] 7 (, + ) 8 [ 2, 0) (0, + ) 0 (, 2) (2, + ) { a + b, kai 7, Raskite
Printing AtvirkstineMatrica.wxmx
 AtvirkstineMatrica.wxmx / Atvirkštinė matrica A.Domarkas, VU, Teoriją žr. [], 8-; []. Figure : Toliau pateiksime atvirkštinės matricos apskaičiavimo būdus su CAS Maxima. su komanda invert pavyzdys. [],
AtvirkstineMatrica.wxmx / Atvirkštinė matrica A.Domarkas, VU, Teoriją žr. [], 8-; []. Figure : Toliau pateiksime atvirkštinės matricos apskaičiavimo būdus su CAS Maxima. su komanda invert pavyzdys. [],
lec10.dvi
 paskaita. Euklido erdv_es. pibr_ezimas. Vektorin_e erdv_e E virs realiuju skaiciu kuno vadinama Euklido erdve, jeigu joje apibr_ezta skaliarin_e sandauga, t.y. tokia funkcija, kuri vektoriu porai u; v
paskaita. Euklido erdv_es. pibr_ezimas. Vektorin_e erdv_e E virs realiuju skaiciu kuno vadinama Euklido erdve, jeigu joje apibr_ezta skaliarin_e sandauga, t.y. tokia funkcija, kuri vektoriu porai u; v
G E O M E T R I J A Gediminas STEPANAUSKAS Turinys 1 TIES ES IR PLOK TUMOS Plok²tumos ir tieses plok²tumoje normalines lygtys
 G E O M E T R I J A Gediminas STEPANAUSKAS 016 09 1 Turinys 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir tieses plok²tumoje normalines lygtys 111 Vektorine forma 11 Koordinatine forma 3 1 Bendroji plok²tumos
G E O M E T R I J A Gediminas STEPANAUSKAS 016 09 1 Turinys 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir tieses plok²tumoje normalines lygtys 111 Vektorine forma 11 Koordinatine forma 3 1 Bendroji plok²tumos
GRAFŲ TEORIJA Pasirenkamasis kursas, Magistrantūra, 3 sem m. rudens semestras Parengė: Eugenijus Manstavičius Įvadas Pirmoji kurso dalis skirta
 GRAFŲ TEORIJA Pasirenkamasis kursas, Magistrantūra, 3 sem. 2018 m. rudens semestras Parengė: Eugenijus Manstavičius Įvadas Pirmoji kurso dalis skirta grafų algoritmams, tačiau apibrėžus gretimumo matricą
GRAFŲ TEORIJA Pasirenkamasis kursas, Magistrantūra, 3 sem. 2018 m. rudens semestras Parengė: Eugenijus Manstavičius Įvadas Pirmoji kurso dalis skirta grafų algoritmams, tačiau apibrėžus gretimumo matricą
Microsoft PowerPoint Dvi svarbios ribos [Read-Only]
![Microsoft PowerPoint Dvi svarbios ribos [Read-Only] Microsoft PowerPoint Dvi svarbios ribos [Read-Only]](/thumbs/88/116285598.jpg) Dvi svarbios ribos Nykstamųjų funkcijų palyginimas. Ekvivalenčios nykstamosios funkcijos. Funkcijos tolydumo taške apibrėžimas. Tolydžiųjų funkcijų atkarpoje savybės. Trūkiosios funkcijos. Trūko taškų
Dvi svarbios ribos Nykstamųjų funkcijų palyginimas. Ekvivalenčios nykstamosios funkcijos. Funkcijos tolydumo taške apibrėžimas. Tolydžiųjų funkcijų atkarpoje savybės. Trūkiosios funkcijos. Trūko taškų
III. SVEIKI NENEIGIAMI SKAIČIAI 3.1 Indukcijos aksioma Natūraliu ju skaičiu aibės sa voka viena svarbiausiu matematikoje. Nors natūralaus skaičiaus sa
 III SVEIKI NENEIGIAMI SKAIČIAI 31 Indukcijos aksioma Natūraliu aibės sa voka viena svarbiausiu matematikoje Nors natūralaus skaičiaus sa voka labai sena, bet šio skaičiaus buveinės sa voka buvo suformuluota
III SVEIKI NENEIGIAMI SKAIČIAI 31 Indukcijos aksioma Natūraliu aibės sa voka viena svarbiausiu matematikoje Nors natūralaus skaičiaus sa voka labai sena, bet šio skaičiaus buveinės sa voka buvo suformuluota
QR algoritmas paskaita
 Turinys QR algoritmas 4 paskaita Olga Štikonienė Diferencialinių lygčių ir skaičiavimo matematikos katedra, MIF VU 4 5 TA skaitiniai metodai ( MIF VU) Tiesinių lygčių sistemų sprendimas / 40 TA skaitiniai
Turinys QR algoritmas 4 paskaita Olga Štikonienė Diferencialinių lygčių ir skaičiavimo matematikos katedra, MIF VU 4 5 TA skaitiniai metodai ( MIF VU) Tiesinių lygčių sistemų sprendimas / 40 TA skaitiniai
Neiškiliojo optimizavimo algoritmas su nauju bikriteriniu potencialiųjų simpleksų išrinkimu naudojant Lipšico konstantos įvertį
 Neiškiliojo optimizavimo algoritmas su nauju bikriteriniu potencialiųjų simpleksų išrinkimu naudojant Lipšico konstantos įvertį. Albertas Gimbutas 2018 m. birželio 19 d. Vadovas: Prof. habil. dr. Antanas
Neiškiliojo optimizavimo algoritmas su nauju bikriteriniu potencialiųjų simpleksų išrinkimu naudojant Lipšico konstantos įvertį. Albertas Gimbutas 2018 m. birželio 19 d. Vadovas: Prof. habil. dr. Antanas
1. Matematinės dėlionės Įvadas Šiame modulyje pateiktos įvairaus sudėtingumo matematinės dėlionės. Jos padės mokytis skaičiuoti mintinai ir rasti įvai
 Įvadas Šiame modulyje pateiktos įvairaus sudėtingumo matematinės dėlionės. Jos padės mokytis skaičiuoti mintinai ir rasti įvairias sprendimo galimybes. Prieš kiekvieną naujos rūšies dėlionę pateiktas pavyzdys,
Įvadas Šiame modulyje pateiktos įvairaus sudėtingumo matematinės dėlionės. Jos padės mokytis skaičiuoti mintinai ir rasti įvairias sprendimo galimybes. Prieš kiekvieną naujos rūšies dėlionę pateiktas pavyzdys,
Microsoft Word - Liuminescencija_teorija
 2. BOLOGNŲ OBJEKTŲ LUMNESCENCJA. 2.1 Įvadas. Liuminescencijos reiškinys Daugelis fotofizikinių ir fotocheminių vyksmų yra šviesos sąveikos su bioobjektu pasekmės. Vienas iš pagrindinių šviesos emisijos
2. BOLOGNŲ OBJEKTŲ LUMNESCENCJA. 2.1 Įvadas. Liuminescencijos reiškinys Daugelis fotofizikinių ir fotocheminių vyksmų yra šviesos sąveikos su bioobjektu pasekmės. Vienas iš pagrindinių šviesos emisijos
Algoritmø analizës specialieji skyriai
 VGTU Matematinio modeliavimo katedra VGTU SC Lygiagrečiųjų skaičiavimų laboratorija Paskaitų kursas. 5-oji dalis. Turinys 1 2 KPU euristiniai sprendimo algoritmai KPU sprendimas dinaminio programavimo
VGTU Matematinio modeliavimo katedra VGTU SC Lygiagrečiųjų skaičiavimų laboratorija Paskaitų kursas. 5-oji dalis. Turinys 1 2 KPU euristiniai sprendimo algoritmai KPU sprendimas dinaminio programavimo
Algoritmai ir duomenų struktūros (ADS) 2 paskaita Saulius Ragaišis, VU MIF
 Algoritmai ir duomenų struktūros (ADS) 2 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2016-02-15 Tiesinės duomenų struktūros Panagrinėsime keletą žinomų ir įvairiuose taikymuose naudojamų
Algoritmai ir duomenų struktūros (ADS) 2 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2016-02-15 Tiesinės duomenų struktūros Panagrinėsime keletą žinomų ir įvairiuose taikymuose naudojamų
MATEMATIKOS BRANDOS EGZAMINO PROGRAMOS MINIMALIUS REIKALAVIMUS ILIUSTRUOJANTYS PAVYZDŽIAI Egzamino programos minimalūs reikalavimai 1.3. Paprastais at
 MTEMTIKS BRNDS EGZMIN PRGRMS MINIMLIUS REIKLVIMUS ILIUSTRUJNTYS PVYZDŽII Egzamino programos minimalūs reikalavimai.. Paprastais atvejais patikrinti, ar duotoji seka ra aritmetinė/geometrinė progresija.
MTEMTIKS BRNDS EGZMIN PRGRMS MINIMLIUS REIKLVIMUS ILIUSTRUJNTYS PVYZDŽII Egzamino programos minimalūs reikalavimai.. Paprastais atvejais patikrinti, ar duotoji seka ra aritmetinė/geometrinė progresija.
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Atsitiktinės paieškos optimizavimo algoritmų vertinimas Evaluat
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Atsitiktinės paieškos optimizavimo algoritmų vertinimas Evaluation of Random Search Optimization Algorithms Magistro
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Atsitiktinės paieškos optimizavimo algoritmų vertinimas Evaluation of Random Search Optimization Algorithms Magistro
Duomenų vizualizavimas
 Duomenų vizualizavimas Daugiamačių duomenų vizualizavimas: projekcijos metodai Aušra Mackutė-Varoneckienė Tomas Krilavičius 1 Projekcijos metodai Analizuojant daugiamačius objektus, kuriuos apibūdina n
Duomenų vizualizavimas Daugiamačių duomenų vizualizavimas: projekcijos metodai Aušra Mackutė-Varoneckienė Tomas Krilavičius 1 Projekcijos metodai Analizuojant daugiamačius objektus, kuriuos apibūdina n
DĖL APLINKOS IR SVEIKATOS MOKSLO KOMITETO ĮSTEIGIMO
 LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRAS ĮSAKYMAS DĖL LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRO 011 M. KOVO D. ĮSAKYMO NR. V-199 DĖL LIETUVOS HIGIENOS NORMOS HN 80:011 ELEKTROMAGNETINIS
LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRAS ĮSAKYMAS DĖL LIETUVOS RESPUBLIKOS SVEIKATOS APSAUGOS MINISTRO 011 M. KOVO D. ĮSAKYMO NR. V-199 DĖL LIETUVOS HIGIENOS NORMOS HN 80:011 ELEKTROMAGNETINIS
Slide 1
 Duomenų struktūros ir algoritmai 2 paskaita 2019-02-13 Algoritmo sąvoka Algoritmas tai tam tikra veiksmų seka, kurią reikia atlikti norint gauti rezultatą. Įvesties duomenys ALGORITMAS Išvesties duomenys
Duomenų struktūros ir algoritmai 2 paskaita 2019-02-13 Algoritmo sąvoka Algoritmas tai tam tikra veiksmų seka, kurią reikia atlikti norint gauti rezultatą. Įvesties duomenys ALGORITMAS Išvesties duomenys
Priedai_2016.indd
 1 testo užduočių vertinimo kriterijai Užd. Nr. Sprendimas ar atsakymas Taškai Vertinimas 1 Pasirinktas variantas D 1 Už teisingą atsakymą. 2 a) 939 1 Už teisingą atsakymą. 2 b) 1538 1 Už teisingą atsakymą.
1 testo užduočių vertinimo kriterijai Užd. Nr. Sprendimas ar atsakymas Taškai Vertinimas 1 Pasirinktas variantas D 1 Už teisingą atsakymą. 2 a) 939 1 Už teisingą atsakymą. 2 b) 1538 1 Už teisingą atsakymą.
Atranka į 2019 m. Pasaulinę ir Vidurio Europos matematikos olimpiadas Sprendimai Artūras Dubickas ir Aivaras Novikas 1. Mykolas sugalvojo natūraliųjų
 Atranka į 019 m. Pasaulinę ir Vidurio Europos matematikos olimpiadas Sprendimai Artūras Dubickas ir Aivaras Novikas 1. Mykolas sugalvojo natūraliųjų skaičių seką a 1, a, a 3,..., o tada apibrėžė naują
Atranka į 019 m. Pasaulinę ir Vidurio Europos matematikos olimpiadas Sprendimai Artūras Dubickas ir Aivaras Novikas 1. Mykolas sugalvojo natūraliųjų skaičių seką a 1, a, a 3,..., o tada apibrėžė naują
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS
 ALEKSANDRO STULGINSKIO UNIVERSITETAS Agronomijos fakultetas Žemdirbystės katedra STUDIJŲ DALYKO APRAŠAS Dalyko kodas: AFŽEB07E Pavadinimas lietuvių kalba: Mokslinių tyrimų metodika Pavadinimas anglų kalba:
ALEKSANDRO STULGINSKIO UNIVERSITETAS Agronomijos fakultetas Žemdirbystės katedra STUDIJŲ DALYKO APRAŠAS Dalyko kodas: AFŽEB07E Pavadinimas lietuvių kalba: Mokslinių tyrimų metodika Pavadinimas anglų kalba:
VERSLO IR VADYBOS TECHNOLOGIJŲ PROGRAMA
 PATVIRTINTA Lietuvos Respublikos švietimo ir mokslo ministro 2007 m. rugsėjo 6 d. įsakymu Nr. ISAK-1790 VERSLO IR VADYBOS TECHNOLOGIJŲ BENDROJI PROGRAMA MOKINIAMS, BESIMOKANTIEMS PAGAL VIDURINIO UGDYMO
PATVIRTINTA Lietuvos Respublikos švietimo ir mokslo ministro 2007 m. rugsėjo 6 d. įsakymu Nr. ISAK-1790 VERSLO IR VADYBOS TECHNOLOGIJŲ BENDROJI PROGRAMA MOKINIAMS, BESIMOKANTIEMS PAGAL VIDURINIO UGDYMO
Dažniausios IT VBE klaidos
 Dažniausios IT VBE klaidos Renata Burbaitė renata.burbaite@gmail.com Kauno technologijos universitetas, Panevėžio Juozo Balčikonio gimnazija 1 Egzamino matrica (iš informacinių technologijų brandos egzamino
Dažniausios IT VBE klaidos Renata Burbaitė renata.burbaite@gmail.com Kauno technologijos universitetas, Panevėžio Juozo Balčikonio gimnazija 1 Egzamino matrica (iš informacinių technologijų brandos egzamino
LIETUVOS RESPUBLIKOS REGIONINĖS PLĖTROS ĮSTATYMO NR. VIII-1889 PAKEITIMO ĮSTATYMAS 2014 m. rugsėjo 18 d. Nr. XII-1094 Vilnius 1 straipsnis. Lietuvos R
 LIETUVOS RESPUBLIKOS REGIONINĖS PLĖTROS ĮSTATYMO NR. VIII-1889 PAKEITIMO ĮSTATYMAS 2014 m. rugsėjo 18 d. Nr. XII-1094 Vilnius 1 straipsnis. Lietuvos Respublikos regioninės plėtros įstatymo Nr. VIII-1889
LIETUVOS RESPUBLIKOS REGIONINĖS PLĖTROS ĮSTATYMO NR. VIII-1889 PAKEITIMO ĮSTATYMAS 2014 m. rugsėjo 18 d. Nr. XII-1094 Vilnius 1 straipsnis. Lietuvos Respublikos regioninės plėtros įstatymo Nr. VIII-1889
LIETUVIŲ KALBOS IR LITERATŪROS MOKYKLINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA
 Projektas PATVRTNTA Nacionalinio egzaminų centro direktoriaus 08 m. lapkričio d. įsakymu Nr. (..)-V- LETUVŲ KALBOS R LTERATŪROS VALSTYBNO BRANDOS EGZAMNO UŽDUOTES VERTNMO KRTERJA. Literatūrinio rašinio
Projektas PATVRTNTA Nacionalinio egzaminų centro direktoriaus 08 m. lapkričio d. įsakymu Nr. (..)-V- LETUVŲ KALBOS R LTERATŪROS VALSTYBNO BRANDOS EGZAMNO UŽDUOTES VERTNMO KRTERJA. Literatūrinio rašinio
TAIKOMOJI MATEMATIKA. 1-ojo testo pavyzdžiai serija **** variantas 001 x x + 12 lim = x 4 2x 8 1 2; 3 0; 2 1 2; 5 1; 6 2; 7 ; riba nee
 001 x 1 2 + x + 12 lim x 4 2x 1 2; 0; 2 1 2; 5 1; 6 2; ; 1 2 4 riba neegzistuoja; 14x 2 2 + 29 lim x 1x 2 + 4x + 9 1 1; 2 29 9 ; ; 4 0; 5 riba neegzistuoja; 6 1 14; 14 1; 14 x + 1 lim x 4 x 4 1 riba neegzistuoja;
001 x 1 2 + x + 12 lim x 4 2x 1 2; 0; 2 1 2; 5 1; 6 2; ; 1 2 4 riba neegzistuoja; 14x 2 2 + 29 lim x 1x 2 + 4x + 9 1 1; 2 29 9 ; ; 4 0; 5 riba neegzistuoja; 6 1 14; 14 1; 14 x + 1 lim x 4 x 4 1 riba neegzistuoja;
Projektas
 PATVIRTINTA Kauno technologijos universiteto Lietuvos socialinių tyrimų centro Vytauto Didžiojo universiteto Sociologijos mokslo krypties doktorantūros komiteto 2019 m. gegužės 8 d. posėdžio nutarimu Nr.
PATVIRTINTA Kauno technologijos universiteto Lietuvos socialinių tyrimų centro Vytauto Didžiojo universiteto Sociologijos mokslo krypties doktorantūros komiteto 2019 m. gegužės 8 d. posėdžio nutarimu Nr.
Individualus projektas Programa TE-PM, TE-PS, TE-SL, TEstream 4, TEstream 6, TEstream 8, TEstreamOBD 4, TEstreamOBD 6, TEstreamOBD 8 sistemų naudotoja
 Individualus projektas Programa TE-PM, TE-PS, TE-SL, TEstream 4, TEstream 6, TEstream 8, TEstreamOBD 4, TEstreamOBD 6, TEstreamOBD 8 sistemų naudotojams Alternatyvus valdymo pultas telefone ViPGaS programos
Individualus projektas Programa TE-PM, TE-PS, TE-SL, TEstream 4, TEstream 6, TEstream 8, TEstreamOBD 4, TEstreamOBD 6, TEstreamOBD 8 sistemų naudotojams Alternatyvus valdymo pultas telefone ViPGaS programos
24 VERSLO APSKAITOS STANDARTO MR
 Audito, apskaitos, turto vertinimo ir nemokumo valdymo tarnyba PATVIRTINTA Audito, apskaitos, turto vertinimo ir nemokumo valdymo tarnybos prie Lietuvos Respublikos finansų ministerijos direktoriaus 2016
Audito, apskaitos, turto vertinimo ir nemokumo valdymo tarnyba PATVIRTINTA Audito, apskaitos, turto vertinimo ir nemokumo valdymo tarnybos prie Lietuvos Respublikos finansų ministerijos direktoriaus 2016
Microsoft Word - 8 Laboratorinis darbas.doc
 Laboratorinis darbas Nr. 8 MOP (metalo sido puslaidininkio) struktūrų tyrimas aukštadažniu -V charakteristikų metodu Darbo tikslas: 1. Nustatyti puslaidininkio laidumo tipą. 2. Nustatyti legiravimo priemaišų
Laboratorinis darbas Nr. 8 MOP (metalo sido puslaidininkio) struktūrų tyrimas aukštadažniu -V charakteristikų metodu Darbo tikslas: 1. Nustatyti puslaidininkio laidumo tipą. 2. Nustatyti legiravimo priemaišų
Slide 1
 Dalelių filtro metodo ir vizualios odometrijos taikymas BPO lokalizacijai 2014 2018 m. studijos Doktorantas: Rokas Jurevičius Vadovas: Virginijus Marcinkevičius Disertacijos tikslas ir objektas Disertacijos
Dalelių filtro metodo ir vizualios odometrijos taikymas BPO lokalizacijai 2014 2018 m. studijos Doktorantas: Rokas Jurevičius Vadovas: Virginijus Marcinkevičius Disertacijos tikslas ir objektas Disertacijos
Tiesioginio-debeto-paslaugos-duomenu-apsikeitimo-formatu-aprasas
 TIEIOGINIO DEBETO PALAUGO DUOMENŲ APIKEITIMO FORMATŲ APRAŠA Tarp banko ir kliento yra keičiamasi tokio tipo failais: utikimai mokėti tiesioginio debeto būdu, priimti įmonėje (failo plėtinys.dse). o Banko
TIEIOGINIO DEBETO PALAUGO DUOMENŲ APIKEITIMO FORMATŲ APRAŠA Tarp banko ir kliento yra keičiamasi tokio tipo failais: utikimai mokėti tiesioginio debeto būdu, priimti įmonėje (failo plėtinys.dse). o Banko
VADOVĖLIO VERTINIMO KRITERIJŲ APRAŠAI 1. MEDŽIAGOS TINKAMUMAS VERTYBINĖMS NUOSTATOMS UGDYTI(S) Vertinimo kriterijai 1.1. Tekstinė ir vaizdinė medžiaga
 VADOVĖLIO VERTINIMO KRITERIJŲ APRAŠAI 1. MEDŽIAGOS TINKAMUMAS VERTYBINĖMS NUOSTATOMS UGDYTI(S) 1.1. Tekstinė ir vaizdinė medžiaga atitinka pagrindines demokratijos vertybes ir principus (asmens ir tautos
VADOVĖLIO VERTINIMO KRITERIJŲ APRAŠAI 1. MEDŽIAGOS TINKAMUMAS VERTYBINĖMS NUOSTATOMS UGDYTI(S) 1.1. Tekstinė ir vaizdinė medžiaga atitinka pagrindines demokratijos vertybes ir principus (asmens ir tautos
21. Ilgis, plotas, perimetras Įvadas Šiame modulyje pateikti įvairaus sudėtingumo uždaviniai apie ilgį, perimetrą ir plotą. Sprendžiant uždavinius rei
 Įvadas Šiame modulyje pateikti įvairaus sudėtingumo uždaviniai apie ilgį, perimetrą ir plotą. Sprendžiant uždavinius reikės pasitelkti kūrybinį mąstymą ir pasinaudoti jau turimomis žiniomis, įgytomis per
Įvadas Šiame modulyje pateikti įvairaus sudėtingumo uždaviniai apie ilgį, perimetrą ir plotą. Sprendžiant uždavinius reikės pasitelkti kūrybinį mąstymą ir pasinaudoti jau turimomis žiniomis, įgytomis per
DISKREČIOJI MATEMATIKA. Grafai serija 5800 variantas 001 Grafas G 1 = (V, B 1 ) apibrėžtas savo viršūnių bei briaunų aibėmis: V = {i, p, z, u, e, s},
 DISKREČIOJI MATEMATIKA. Grafai serija 5800 variantas 001 Grafas G 1 = (V, B 1 ) apibrėžtas savo viršūnių bei briaunų aibėmis: V = {i, p, z, u, e, s}, B 1 = {{i, p}, {i, e}, {z, e}, {u, e}, {u, s}}. Grafai
DISKREČIOJI MATEMATIKA. Grafai serija 5800 variantas 001 Grafas G 1 = (V, B 1 ) apibrėžtas savo viršūnių bei briaunų aibėmis: V = {i, p, z, u, e, s}, B 1 = {{i, p}, {i, e}, {z, e}, {u, e}, {u, s}}. Grafai
Printing triistr.wxmx
 triistr.wxmx / Triįstrižainių lygčių sistemų sprendimas A.Domarkas, VU, Teoriją žr. []; [], 7-7; []. Pradžioje naudosime Gauso algoritmą, kuriame po įstrižaine daromi nuliai. Po to grįždami į viršų virš
triistr.wxmx / Triįstrižainių lygčių sistemų sprendimas A.Domarkas, VU, Teoriją žr. []; [], 7-7; []. Pradžioje naudosime Gauso algoritmą, kuriame po įstrižaine daromi nuliai. Po to grįždami į viršų virš
(Microsoft Word - pasiekim\370 tvarka 2018.doc)
 PATVIRTINTA Druskininkų Ryto gimnazijos direktoriaus 2017 m. rugpjūčio 28 d. įsakymu Nr. V1 283 (Druskininkų Ryto gimnazijos direktoriaus 2018 m. rugsėjo 5 d. įsakymu Nr. V1-326 redakcija) DRUSKININKŲ
PATVIRTINTA Druskininkų Ryto gimnazijos direktoriaus 2017 m. rugpjūčio 28 d. įsakymu Nr. V1 283 (Druskininkų Ryto gimnazijos direktoriaus 2018 m. rugsėjo 5 d. įsakymu Nr. V1-326 redakcija) DRUSKININKŲ
PowerPoint Presentation
 Montažų kūrimas iš skaitmeninių nuotraukų naudojant Windows Photo Story 3 programą Photo Story 3 Priedas Windows XP, Windows 8, Windows 10 Skirtas kurti dinamiškus fotoreportažus iš turimų skaitmeninių
Montažų kūrimas iš skaitmeninių nuotraukų naudojant Windows Photo Story 3 programą Photo Story 3 Priedas Windows XP, Windows 8, Windows 10 Skirtas kurti dinamiškus fotoreportažus iš turimų skaitmeninių
PowerPoint Presentation
 Valstybinės energetikos inspekcijos vartotojams teikiamų paslaugų kokybės, prieinamumo ir pasitenkinimo tyrimas užsakovas vykdytojas Kovas, 2016 metodologija 2 Tyrimo metodologija Visuomenės nuomonės ir
Valstybinės energetikos inspekcijos vartotojams teikiamų paslaugų kokybės, prieinamumo ir pasitenkinimo tyrimas užsakovas vykdytojas Kovas, 2016 metodologija 2 Tyrimo metodologija Visuomenės nuomonės ir
Masyvas su C++ Užduotys. Išsiaiškinkite kodą (jei reikia pataisykite) ir paleiskite per programą. Ciklo skaitliuko įrašymas į vienmatį masyvą: #includ
 Masyvas su C++ Užduotys. Išsiaiškinkite kodą (jei reikia pataisykite) ir paleiskite per programą. Ciklo skaitliuko įrašymas į vienmatį masyvą: #include main() int mas[100]; int k; for (int
Masyvas su C++ Užduotys. Išsiaiškinkite kodą (jei reikia pataisykite) ir paleiskite per programą. Ciklo skaitliuko įrašymas į vienmatį masyvą: #include main() int mas[100]; int k; for (int
Sistemos specifikacija
 Finansinių ataskaitų rinkinių teikimo elektroniniu būdu (interaktyviai) Vartotojo vadovas Kaip pateikti finansinių ataskaitų rinkinį el. būdu interaktyviai 2(32) Turinys 1. Įvadas...3 2. Finansinių ataskaitų
Finansinių ataskaitų rinkinių teikimo elektroniniu būdu (interaktyviai) Vartotojo vadovas Kaip pateikti finansinių ataskaitų rinkinį el. būdu interaktyviai 2(32) Turinys 1. Įvadas...3 2. Finansinių ataskaitų
Projektas
 PATVIRTINTA Kauno technologijos universiteto Lietuvos socialinių tyrimų centro Vytauto Didžiojo universiteto Sociologijos mokslo krypties doktorantūros komiteto 2017 m. birželio 6 d. posėdžio nutarimu
PATVIRTINTA Kauno technologijos universiteto Lietuvos socialinių tyrimų centro Vytauto Didžiojo universiteto Sociologijos mokslo krypties doktorantūros komiteto 2017 m. birželio 6 d. posėdžio nutarimu
Longse Wi-Fi kameros greito paleidimo instrukcija 1. Jums prireiks 1.1. Longse Wi-Fi kameros 1.2. Vaizdo stebėjimo kameros maitinimo šaltinio 1.3. UTP
 Longse Wi-Fi kameros greito paleidimo instrukcija 1. Jums prireiks 1.1. Longse Wi-Fi kameros 1.2. Vaizdo stebėjimo kameros maitinimo šaltinio 1.3. UTP RJ-45 interneto kabelio 1.4. Kompiuterio su prieiga
Longse Wi-Fi kameros greito paleidimo instrukcija 1. Jums prireiks 1.1. Longse Wi-Fi kameros 1.2. Vaizdo stebėjimo kameros maitinimo šaltinio 1.3. UTP RJ-45 interneto kabelio 1.4. Kompiuterio su prieiga
VIDURINIO UGDYMAS Vidurinis ugdymas neprivalomas, trunka dvejus metus (11 ir 12 vidurinės mokyklos ar gimnazijų III IV klasės). Mokiniai mokosi pagal
 VIDURINIO UGDYMAS Vidurinis ugdymas neprivalomas, trunka dvejus metus (11 ir 12 vidurinės mokyklos ar gimnazijų III IV klasės). Mokiniai mokosi pagal individualius ugdymosi planus. (Pagal vidurinio ugdymo
VIDURINIO UGDYMAS Vidurinis ugdymas neprivalomas, trunka dvejus metus (11 ir 12 vidurinės mokyklos ar gimnazijų III IV klasės). Mokiniai mokosi pagal individualius ugdymosi planus. (Pagal vidurinio ugdymo
Slide 1
 Avansinio pelno mokesčio apskaičiavimo, sumokėjimo ir deklaravimo tvarka VMI prie FM Mokesčių informacijos departamentas 2017 m. Seminaro planas Avansinio pelno mokesčio (toliau avansinis PM) apskaičiavimas
Avansinio pelno mokesčio apskaičiavimo, sumokėjimo ir deklaravimo tvarka VMI prie FM Mokesčių informacijos departamentas 2017 m. Seminaro planas Avansinio pelno mokesčio (toliau avansinis PM) apskaičiavimas
VĮ GIS-Centras Vilnius 2019 Palydovinių duomenų peržiūros ir analizės paslauga Naudotojo vadovas v.1
 VĮ GIS-Centras Vilnius 2019 Palydovinių duomenų peržiūros ir analizės paslauga Naudotojo vadovas v.1 Turinys ĮŽANGA... 3 1. PALYDOVINIŲ DUOMENŲ PERŽIŪROS IR ANALIZĖS PASLAUGA... 4 1.1. Paslaugos apžvalga...
VĮ GIS-Centras Vilnius 2019 Palydovinių duomenų peržiūros ir analizės paslauga Naudotojo vadovas v.1 Turinys ĮŽANGA... 3 1. PALYDOVINIŲ DUOMENŲ PERŽIŪROS IR ANALIZĖS PASLAUGA... 4 1.1. Paslaugos apžvalga...
1. Druskininkų savivaldybės nekilnojamojo turto rinkos apžvalga 2017 m. Druskininkų savivaldybė yra suskirstyta į 16 nekilnojamojo turto verčių zonų,
 1. Druskininkų savivaldybės nekilnojamojo turto rinkos apžvalga 217 m. Druskininkų savivaldybė yra suskirstyta į 16 nekilnojamojo turto verčių zonų, kuriose nekilnojamojo turto kainos yra skirtingos. segmente,
1. Druskininkų savivaldybės nekilnojamojo turto rinkos apžvalga 217 m. Druskininkų savivaldybė yra suskirstyta į 16 nekilnojamojo turto verčių zonų, kuriose nekilnojamojo turto kainos yra skirtingos. segmente,
DB sukūrimas ir užpildymas duomenimis
 DB sukūrimas ir užpildymas duomenimis Duomenų bazės kūrimas Naujas bendrąsias DB kuria sistemos administratorius. Lokalias DB gali kurti darbo stoties vartotojasadministratorius. DB kuriama: kompiuterio
DB sukūrimas ir užpildymas duomenimis Duomenų bazės kūrimas Naujas bendrąsias DB kuria sistemos administratorius. Lokalias DB gali kurti darbo stoties vartotojasadministratorius. DB kuriama: kompiuterio
Lietuvos mobiliojo ryšio operatorių 30Mbit/s zonų skaičiavimo metodika
 MOBILIOJO RYŠIO OPERATORIŲ 30 MB/S APRĖPTIES SKAIČIAVIMAI RRT atliktos analizės rezultatų viešas aptarimas, Susisiekimo ministerija 2015 10 19 Lietuvos respublikos ryšių reguliavimo tarnyba Direktoriaus
MOBILIOJO RYŠIO OPERATORIŲ 30 MB/S APRĖPTIES SKAIČIAVIMAI RRT atliktos analizės rezultatų viešas aptarimas, Susisiekimo ministerija 2015 10 19 Lietuvos respublikos ryšių reguliavimo tarnyba Direktoriaus
Microsoft PowerPoint - ikaitinti_kunai02.ppt
 Šviesos šaltiniai Nekoherentiniai šviesos šaltiniai. Šviesos šaltinių rūšys. Absoliučiai juodo kūno spinduliavimas. Kaitinimo lempos. Dujų išlydžio lempos. Šviestukų veikimo fizikiniai principai ir technologijos.
Šviesos šaltiniai Nekoherentiniai šviesos šaltiniai. Šviesos šaltinių rūšys. Absoliučiai juodo kūno spinduliavimas. Kaitinimo lempos. Dujų išlydžio lempos. Šviestukų veikimo fizikiniai principai ir technologijos.
Projektas „Europos kreditų perkėlimo ir kaupimo sistemos (ECTS) nacionalinės koncepcijos parengimas: kreditų harmonizavimas ir mokymosi pasiekimais gr
 Studijų programos aprašas Studijų programos pavadinimas Informatika Aukštojo mokslo institucija (-os), padalinys (-iai) Vilniaus universitetas, Matematikos ir informatikos fakultetas, Informatikos katedra
Studijų programos aprašas Studijų programos pavadinimas Informatika Aukštojo mokslo institucija (-os), padalinys (-iai) Vilniaus universitetas, Matematikos ir informatikos fakultetas, Informatikos katedra
Projektą vykdančiojo personalo darbo užmokesčio ir savanoriško darbo įnašo fiksuotojo įkainio nustatymo tyrimo ataskaita 2016 m. birželio 8 d. redakci
 Projektą vykdančiojo personalo darbo užmokesčio ir savanoriško darbo įnašo fiksuotojo įkainio nustatymo tyrimo ataskaita 2016 m. birželio 8 d. redakcija Lietuvos Respublikos vidaus reikalų ministerija
Projektą vykdančiojo personalo darbo užmokesčio ir savanoriško darbo įnašo fiksuotojo įkainio nustatymo tyrimo ataskaita 2016 m. birželio 8 d. redakcija Lietuvos Respublikos vidaus reikalų ministerija
Logines funkcijos termu generavimo algoritmas pagristas funkciniu modeliu
 KAUNO TECHNOLOGIJOS UNIVERSITETAS INFORMATIKOS FAKULTETAS PROGRAMŲ INŽINERIJOS KATEDRA Tomas Žemaitis LOGINĖS FUNKCIJOS TERMŲ GENERAVIMO ALGORITMAS PAGRĮSTAS PROGRAMINIO PROTOTIPO MODELIU Magistro darbas
KAUNO TECHNOLOGIJOS UNIVERSITETAS INFORMATIKOS FAKULTETAS PROGRAMŲ INŽINERIJOS KATEDRA Tomas Žemaitis LOGINĖS FUNKCIJOS TERMŲ GENERAVIMO ALGORITMAS PAGRĮSTAS PROGRAMINIO PROTOTIPO MODELIU Magistro darbas
airbnb-pwc-taxguide-lithuania-lt
 Šį vadovą parengė nepriklausoma apskaitos įmonė 2018 m. rugsėjo LIETUVA SU TRUMPALAIKE NUOMA SUSIJĘ MOKESČIŲ KLAUSIMAI Toliau pateikta informacija yra gairės, padėsiančios susipažinti su kai kuriais mokesčių
Šį vadovą parengė nepriklausoma apskaitos įmonė 2018 m. rugsėjo LIETUVA SU TRUMPALAIKE NUOMA SUSIJĘ MOKESČIŲ KLAUSIMAI Toliau pateikta informacija yra gairės, padėsiančios susipažinti su kai kuriais mokesčių
Gabių vaikų ugdymo mokymo priemonių dokumentas parengtas, įgyvendinant ES lėšomis finansuojamą projektą Gabių vaikų ugdymo efekytyvumo didinimas šviet
 61 rogramos 1.5 temos nalizuoti ir prognozuoti vartotojų reakciją į kainų pokytį, remiantis paklausos elastingumu kainoms, ir gamintojų reakciją į kainų pokytį, remiantis pasiūlos elastingumu kainoms raplėtimas
61 rogramos 1.5 temos nalizuoti ir prognozuoti vartotojų reakciją į kainų pokytį, remiantis paklausos elastingumu kainoms, ir gamintojų reakciją į kainų pokytį, remiantis pasiūlos elastingumu kainoms raplėtimas
L I E T U V O S J A U N Ų J Ų M A T E M A T I K Ų M O K Y K L A 2. TRIKAMPIŲ ČEVIANOS ( ) Teorinę medžiagą parengė ir antrąją užduotį sudarė V
 L I T U V O S J U N Ų J Ų T T I K Ų O K Y K L. TRIKPIŲ ČVINOS (017 019) Teorinę medžiagą parengė ir antrąją užduotį sudarė Vilniaus universiteto docentas dmundas azėtis atematikos pamokose nagrinėjamos
L I T U V O S J U N Ų J Ų T T I K Ų O K Y K L. TRIKPIŲ ČVINOS (017 019) Teorinę medžiagą parengė ir antrąją užduotį sudarė Vilniaus universiteto docentas dmundas azėtis atematikos pamokose nagrinėjamos
PowerPoint Presentation
 Duomenų archyvai ir mokslo duomenų valdymo planai 2018-06-13 1 Re3Data duomenų talpyklų registras virš 2000 mokslinių tyrimų duomenų talpyklų; talpyklos paiešką galima atlikti pagal mokslo kryptį, šalį,
Duomenų archyvai ir mokslo duomenų valdymo planai 2018-06-13 1 Re3Data duomenų talpyklų registras virš 2000 mokslinių tyrimų duomenų talpyklų; talpyklos paiešką galima atlikti pagal mokslo kryptį, šalį,
File Transfer programinės įrangos naudotojo instrukcija
 File Transfer programinės įrangos naudotojo instrukcija Rinkmenos dalių įkėlimas naudojantis i.saf-t FileTransfer FileTransfer programinė įranga (toliau - FileTransfer PĮ) skirta didelės apimties rinkmenos
File Transfer programinės įrangos naudotojo instrukcija Rinkmenos dalių įkėlimas naudojantis i.saf-t FileTransfer FileTransfer programinė įranga (toliau - FileTransfer PĮ) skirta didelės apimties rinkmenos
Kauno menų darželis Etiudas Mgr. Virginija Bielskienė, direktorės pavaduotoja ugdymui, II vad. kategorija, auklėtoja metodininkė Žaidimas pagrindinė i
 Kauno menų darželis Etiudas Mgr. Virginija Bielskienė, direktorės pavaduotoja ugdymui, II vad. kategorija, auklėtoja metodininkė Žaidimas pagrindinė ikimokyklinio ir priešmokyklinio amžiaus ir jaunesnio
Kauno menų darželis Etiudas Mgr. Virginija Bielskienė, direktorės pavaduotoja ugdymui, II vad. kategorija, auklėtoja metodininkė Žaidimas pagrindinė ikimokyklinio ir priešmokyklinio amžiaus ir jaunesnio
Projektas
 1 PRIEDAS PATVIRTINTA Vytauto Didžiojo universiteto Menotyros mokslo krypties doktorantūros komiteto 2019 m. gegužės 28 d. posėdžio nutarimu Nr.1 ATVIRO KONKURSO Į MENOTYROS MOKSLO KRYPTIES DOKTORANTŪROS
1 PRIEDAS PATVIRTINTA Vytauto Didžiojo universiteto Menotyros mokslo krypties doktorantūros komiteto 2019 m. gegužės 28 d. posėdžio nutarimu Nr.1 ATVIRO KONKURSO Į MENOTYROS MOKSLO KRYPTIES DOKTORANTŪROS
GKTR :2014
 GKTR 2.11.03:2014 Geroji naujiena ar tas pats galvos skausmas? A. Balsevičius, LGMS sekretorius LGMS visuotinis susirinkimas 2014m. kovo 28d. Topografinių erdvinių objektų rinkinys ir topografinių erdvinių
GKTR 2.11.03:2014 Geroji naujiena ar tas pats galvos skausmas? A. Balsevičius, LGMS sekretorius LGMS visuotinis susirinkimas 2014m. kovo 28d. Topografinių erdvinių objektų rinkinys ir topografinių erdvinių
Slide 1
 Duomenų struktūros ir algoritmai 12 paskaita 2019-05-08 Norint kažką sukonstruoti, reikia... turėti detalių. 13 paskaitos tikslas Susipažinti su python modulio add.py 1.1 versija. Sukurti skaitmeninį modelį
Duomenų struktūros ir algoritmai 12 paskaita 2019-05-08 Norint kažką sukonstruoti, reikia... turėti detalių. 13 paskaitos tikslas Susipažinti su python modulio add.py 1.1 versija. Sukurti skaitmeninį modelį
PowerPoint Presentation
 Dirvožemio erdvinių duomenų rinkinys ir jo praktinis naudojimas 2017 m. Valstybės įmonė Valstybės žemės fondas bendradarbiauja įgyvendinant Lietuvos Respublikos žemės ūkio ministerijos strateginius veiklos
Dirvožemio erdvinių duomenų rinkinys ir jo praktinis naudojimas 2017 m. Valstybės įmonė Valstybės žemės fondas bendradarbiauja įgyvendinant Lietuvos Respublikos žemės ūkio ministerijos strateginius veiklos
Diferencialinių lygčių dalinėmis išvestinėmis sprendimo metodai. Įvadas.
 Turinys Diferencialinių lygčių dalinėmis išvestinėmis sprendimo metodai. Įvadas. Olga Štikonienė Diferencialinių lygčių ir skaičiavimo matematikos katedra, MIF VU 2017-05-29 Egzamino klausimai: 1) Diferencialinės
Turinys Diferencialinių lygčių dalinėmis išvestinėmis sprendimo metodai. Įvadas. Olga Štikonienė Diferencialinių lygčių ir skaičiavimo matematikos katedra, MIF VU 2017-05-29 Egzamino klausimai: 1) Diferencialinės
Algoritmai ir duomenų struktūros (ADS) 7 paskaita Saulius Ragaišis, VU MIF
 Algoritmai ir duomenų struktūros (ADS) 7 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2015-04-13 Grafai Grafas aibių pora (V, L). V viršūnių (vertex) aibė, L briaunų (edge) aibė Briauna
Algoritmai ir duomenų struktūros (ADS) 7 paskaita Saulius Ragaišis, VU MIF saulius.ragaisis@mif.vu.lt 2015-04-13 Grafai Grafas aibių pora (V, L). V viršūnių (vertex) aibė, L briaunų (edge) aibė Briauna
P. Kasparaitis. Praktinė informatika. Skriptų vykdymas ir duomenų valdymas Skriptų vykdymas ir duomenų valdymas Įvadas Skripto failas tai M
 Skriptų vykdymas ir duomenų valdymas Įvadas Skripto failas tai MATLAB komandų seka, vadinama programa, įrašyta į failą. Vykdant skripto failą įvykdomos jame esančios komandos. Bus kalbama, kaip sukurti
Skriptų vykdymas ir duomenų valdymas Įvadas Skripto failas tai MATLAB komandų seka, vadinama programa, įrašyta į failą. Vykdant skripto failą įvykdomos jame esančios komandos. Bus kalbama, kaip sukurti
ES F ben dri Projekto kodas (Įrašoma automatiškai) 1 PROJEKTO SFMIS DUOMENŲ FORMA FORMAI PRITARTA m. Europos Sąjungos struktūrinės paramos a
 ES F ben dri 1 PROJEKTO SFMIS DUOMENŲ FORMA FORMAI PRITARTA 2014-2020 m. Europos Sąjungos struktūrinės paramos administravimo darbo grupės, sudarytos Lietuvos Respublikos finansų ministro 2013 m. liepos
ES F ben dri 1 PROJEKTO SFMIS DUOMENŲ FORMA FORMAI PRITARTA 2014-2020 m. Europos Sąjungos struktūrinės paramos administravimo darbo grupės, sudarytos Lietuvos Respublikos finansų ministro 2013 m. liepos
PATVIRTINTA Elektrėnų pradinės mokyklos direktoriaus 2011 m. rugpjūčio 22 d. įsakymu Nr. 1V 69 ELEKTRĖNŲ PRADINĖS MOKYKLOS MOKINIŲ PAŽANGOS IR PASIEKI
 PATVIRTINTA direktoriaus 2011 m. rugpjūčio 22 d. įsakymu Nr. 1V 69 ELEKTRĖNŲ PRADINĖS MOKYKLOS MOKINIŲ PAŽANGOS IR PASIEKIMŲ VERTINIMO TVARKA I. BENDROSIOS NUOSTATOS 1. (toliau mokyklos) mokinių pažangos
PATVIRTINTA direktoriaus 2011 m. rugpjūčio 22 d. įsakymu Nr. 1V 69 ELEKTRĖNŲ PRADINĖS MOKYKLOS MOKINIŲ PAŽANGOS IR PASIEKIMŲ VERTINIMO TVARKA I. BENDROSIOS NUOSTATOS 1. (toliau mokyklos) mokinių pažangos
RET2000 Elektronisis Skaitmeninis Termostatas su LCD
 MAKING MODERN LIVING POSSIBLE RET2000 B/M/MS Elektroninis skaitmeninis termostatas su LCD Danfoss Heating Montavimo vadovas Norėdami gauti išsamią spausdintą šių instrukcijų versiją, skambinkite Rinkodaros
MAKING MODERN LIVING POSSIBLE RET2000 B/M/MS Elektroninis skaitmeninis termostatas su LCD Danfoss Heating Montavimo vadovas Norėdami gauti išsamią spausdintą šių instrukcijų versiją, skambinkite Rinkodaros
XI skyrius. KŪNAI 1. Kūno sa voka Šiame skyriuje nagrinėsime kūnus. Kūnas tai aibė k, kurioje apibrėžti aibės k elementu du vidiniai kompozicijo
 XI skyrius KŪNAI 1 Kūno sa voka 1 1 Šiame skyriuje nagrinėsime kūnus Kūnas tai aibė k, kurioje apibrėžti aibės k elementu du vidiniai kompozicijos dėsniai, žymimi + ir, ir vadinami aibės k elementu sudėtimi
XI skyrius KŪNAI 1 Kūno sa voka 1 1 Šiame skyriuje nagrinėsime kūnus Kūnas tai aibė k, kurioje apibrėžti aibės k elementu du vidiniai kompozicijos dėsniai, žymimi + ir, ir vadinami aibės k elementu sudėtimi
Printing BaziniaiSprendiniai&KrastutiniaiTaskai.wxm
 BaziniaiSprendiniai&KrastutiniaiTaskai.wxm / Baziniai sprendiniai ir kraštutiniai taškai (C) A.Domarkas, VU, 25 žr.: [] 2-252; [2] 9-98; [3] 33-; [] 89-98; [5] 6.3 Tegul tiesinių lygčių sistemos nežinomųjų
BaziniaiSprendiniai&KrastutiniaiTaskai.wxm / Baziniai sprendiniai ir kraštutiniai taškai (C) A.Domarkas, VU, 25 žr.: [] 2-252; [2] 9-98; [3] 33-; [] 89-98; [5] 6.3 Tegul tiesinių lygčių sistemos nežinomųjų
Microsoft Word - AUTOSERVISO MODULIS
 AUTOSERVISO MODULIS APRAŠYMAS 1. Darbo pradžia. Autoserviso modul aktyvuokite per programos meniu Parametrai > Darbo vietos nustatymai. Skyrelyje Kiti pažymkite Autoservisas ir paspauskite mygtuk Gerai.
AUTOSERVISO MODULIS APRAŠYMAS 1. Darbo pradžia. Autoserviso modul aktyvuokite per programos meniu Parametrai > Darbo vietos nustatymai. Skyrelyje Kiti pažymkite Autoservisas ir paspauskite mygtuk Gerai.
BALSO SKAMBUČIŲ UŽBAIGIMO JUDRIOJO RYŠIO TINKLE SĄNAUDŲ APSKAIČIAVIMO PAAIŠKINIMAS IR SKAMBUČIŲ INICIJAVIMO SĄNAUDŲ SKAIČIAVIMO PRINCIPŲ PAAIŠKINIMAS
 BALSO SKAMBUČIŲ UŽBAIGIMO JUDRIOJO RYŠIO TINKLE SĄNAUDŲ APSKAIČIAVIMO PAAIŠKINIMAS IR SKAMBUČIŲ INICIJAVIMO SĄNAUDŲ SKAIČIAVIMO PRINCIPŲ PAAIŠKINIMAS I. ĮŽANGA Lietuvos Respublikos ryšių reguliavimo tarnybos
BALSO SKAMBUČIŲ UŽBAIGIMO JUDRIOJO RYŠIO TINKLE SĄNAUDŲ APSKAIČIAVIMO PAAIŠKINIMAS IR SKAMBUČIŲ INICIJAVIMO SĄNAUDŲ SKAIČIAVIMO PRINCIPŲ PAAIŠKINIMAS I. ĮŽANGA Lietuvos Respublikos ryšių reguliavimo tarnybos
UAB NAUJASIS TURGUS PREKYBOS VIETŲ KAINOS NUSTATYMO METODIKA UAB Naujasis turgus užsakymu parengė UAB Eurointegracijos projektai Vilnius,
 UAB NAUJASIS TURGUS PREKYBOS VIETŲ KAINOS NUSTATYMO METODIKA UAB Naujasis turgus užsakymu parengė UAB Eurointegracijos projektai Vilnius, 2017 1 UAB NAUJASIS TURGUS PREKYBOS VIETŲ KAINOS NUSTATYMO METODIKA
UAB NAUJASIS TURGUS PREKYBOS VIETŲ KAINOS NUSTATYMO METODIKA UAB Naujasis turgus užsakymu parengė UAB Eurointegracijos projektai Vilnius, 2017 1 UAB NAUJASIS TURGUS PREKYBOS VIETŲ KAINOS NUSTATYMO METODIKA
SKENAVIMO KOMPIUTERINIU TOMOGRAFU PROTOKOLAS
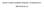 SKENAVIMO KOMPIUTERINIU TOMOGRAFU PROTOKOLAS TURINYS KLUBO SĄNARIO 3D REKONSTRUKCIJA... 3 DUBENKAULIO 3D REKONSTRUKCIJA... 4 KELIO SĄNARIO 3D REKONSTRUKCIJA... 5 PETIES SĄNARIO 3D REKONSTRUKCIJA... 6 KAUKOLĖS
SKENAVIMO KOMPIUTERINIU TOMOGRAFU PROTOKOLAS TURINYS KLUBO SĄNARIO 3D REKONSTRUKCIJA... 3 DUBENKAULIO 3D REKONSTRUKCIJA... 4 KELIO SĄNARIO 3D REKONSTRUKCIJA... 5 PETIES SĄNARIO 3D REKONSTRUKCIJA... 6 KAUKOLĖS
Elektroninio dokumento nuorašas UKMERGĖS RAJONO SAVIVALDYBĖS ADMINISTRACIJOS DIREKTORIUS ĮSAKYMAS DĖL NACIONALINIO MOKINIŲ PASIEKIMŲ PATIKRINIMO (DIAG
 Elektroninio dokumento nuorašas UKMERGĖS RAJONO SAVIVALDYBĖS ADMINISTRACIJOS DIREKTORIUS ĮSAKYMAS DĖL NACIONALINIO MOKINIŲ PASIEKIMŲ PATIKRINIMO (DIAGNOSTINIŲ IR STANDARTIZUOTŲ TESTŲ) ORGANIZAVIMO, VYKDYMO
Elektroninio dokumento nuorašas UKMERGĖS RAJONO SAVIVALDYBĖS ADMINISTRACIJOS DIREKTORIUS ĮSAKYMAS DĖL NACIONALINIO MOKINIŲ PASIEKIMŲ PATIKRINIMO (DIAGNOSTINIŲ IR STANDARTIZUOTŲ TESTŲ) ORGANIZAVIMO, VYKDYMO
Microsoft Word - Ak noretum grizti v04.docx
 Laimutės Kisielienės choreografija Jūratės Baltramiejūnaitės muzika, Bernardo Brazdžionio žodžiai PAKEITIMAI 2015/08/09 Originalas išdalintas šokių kursuose 2015/09/01 Pakeitimai padaryti po šokių kursų
Laimutės Kisielienės choreografija Jūratės Baltramiejūnaitės muzika, Bernardo Brazdžionio žodžiai PAKEITIMAI 2015/08/09 Originalas išdalintas šokių kursuose 2015/09/01 Pakeitimai padaryti po šokių kursų
Techninė dokumentacija Qlik Sense architektūros apžvalga 2015 m. gruodis qlik.com
 Techninė dokumentacija Qlik Sense architektūros apžvalga 2015 m. gruodis qlik.com Platforma Qlik Sense tai analitikos platforma, naudojanti asociatyvinį analitikos variklį operatyvinėje atmintyje. Remiantis
Techninė dokumentacija Qlik Sense architektūros apžvalga 2015 m. gruodis qlik.com Platforma Qlik Sense tai analitikos platforma, naudojanti asociatyvinį analitikos variklį operatyvinėje atmintyje. Remiantis
Microsoft Word - Dokumentas1
 2014 2020 metų Europos Sąjungos fondų investicijų veiksmų programos 3 prioriteto Smulkiojo ir vidutinio verslo konkurencingumo skatinimas priemonės Nr. 03.3.1-LVPA-K-803 Regio Invest LT+ projektų finansavimo
2014 2020 metų Europos Sąjungos fondų investicijų veiksmų programos 3 prioriteto Smulkiojo ir vidutinio verslo konkurencingumo skatinimas priemonės Nr. 03.3.1-LVPA-K-803 Regio Invest LT+ projektų finansavimo
RR-GSM_IM_LT_110125
 Retransliatorius RR-GSM Įrengimo instrukcija Draugystės g. 17, LT-51229 Kaunas El. p.: info@trikdis.lt www.trikdis.lt Retransliatorius RR-GSM perduoda priimtus pranešimus į centralizuoto stebėjimo pultą
Retransliatorius RR-GSM Įrengimo instrukcija Draugystės g. 17, LT-51229 Kaunas El. p.: info@trikdis.lt www.trikdis.lt Retransliatorius RR-GSM perduoda priimtus pranešimus į centralizuoto stebėjimo pultą
Vigirdas Mackevičius 2. Sekos riba Paskaitu konspektas Intuityviai realiu ju skaičiu seka vadinama realiu ju skaičiu aibė, kurios elementai (vadinami
 Vigirdas Mackevičius 2. Sekos riba Paskaitu kospektas Ituityviai realiu seka vadiama realiu aibė, kurios elemetai (vadiami sekos ariais) suumeruoti atūraliaisiais skaičiais (pradedat galbūt e vieetu, o
Vigirdas Mackevičius 2. Sekos riba Paskaitu kospektas Ituityviai realiu seka vadiama realiu aibė, kurios elemetai (vadiami sekos ariais) suumeruoti atūraliaisiais skaičiais (pradedat galbūt e vieetu, o
ĮSIVERTINIMO IR PAŽANGOS ATASKAITA M. M. (2018 M.) Įstaigos kodas Mokyklos pavadinimas Kauno Varpo gimnazija Savivaldybė Kauno m.
 ĮSIVERTINIMO IR PAŽANGOS ATASKAITA 2017 2018 M. M. (2018 M.) Įstaigos kodas 190138895 Mokyklos pavadinimas Kauno Varpo gimnazija Savivaldybė Kauno m. 1. Už kurį laikotarpį pateikiate ataskaitą? (pasirinkite)
ĮSIVERTINIMO IR PAŽANGOS ATASKAITA 2017 2018 M. M. (2018 M.) Įstaigos kodas 190138895 Mokyklos pavadinimas Kauno Varpo gimnazija Savivaldybė Kauno m. 1. Už kurį laikotarpį pateikiate ataskaitą? (pasirinkite)
